５３．ホームランが打ちたい

　昭和時代を3分割していうならば、昭和後期が始まった頃のこと、スポーツ観戦と言えばテレビのプロ野球くらいしかなかった。地域性によるが、六甲おろしが流れていた。通っていた銭湯の下駄箱は、いつも田淵の背番号 22 だった。

　贔屓の球団は、自分が生まれてから一度も優勝していなかった。ところが、大学 2 年のとき、優勝してしまった。21 年振りの優勝であった。中西が最後に投げて優勝を決めた試合は長引き、友達の下宿で翌日のドイツ語の授業の予習会を 4 人で行う曜日だったのだが、さすがに遅れて参加した。祝勝のビールを買い込んで。「どうせ遅れてくると思った」と、広島出身や盛岡出身の友達には大目に見てもらえた。

　バース・掛布・岡田の最強打線の頃だった。それを過ぎると、一度優勝してしまったこともあり、急に興味がしぼんだ。それ以降、高校野球を含めても、あまり野球は見ない。

　ある日、研究室の外線電話が鳴った。どうせ、「東京で投資のマンション買いませんか」の類だろうと思って、極めて不機嫌なトーンで電話に出ると、子供が水泳の全国大会で東京辰巳の国際水泳競技場で泳いでいたが、そっち方向にある信頼のおける某所からの電話で、トーンを戻して話を聞いてみると、ホームランを打つ企画をしているのだが、ホームランを打てない子でも打つ方法は無いものか、しっかり練習して挑戦するのだが、どうしても打てなかった場合、ブログの 50 回にあった「スーパーボールの衝突」なんかを利用して、ホームランが打てない子でも打たせてあげられないものか、との内容の電話であった。スーパーボールは多段階の衝突を考えると、どんどん速さが早くなる（50 回参照）という話だったのだが、さて、それと同じ原理を野球のバットに仕込めるものか、ちょっとアイデアがなかった。とりあえず、野球の統一球は跳ね返り係数（反発係数）が決まっているので、反発係数の大きな素材で実験してみたら、程度の返答しかできず、その旨お話しして電話を措いた。

　言った手前、そのあと、野球のボールをバットで打ったらどうなるかを、反発係数を変えたらどれくらい飛距離が伸びるかを中心に考えてみた。図1 の大きい円がバットの断面、小さい円がボールの断面とする。図で左向きに速さ v [m/s] で飛んできたボールを、バットを右向きに速さ V [m/s] で振って当てる。バットとボールの接触点とバットの中心を結ぶ線が、図のように水平面と角度 θ を持って衝突したとしよう。水平方向をx 方向、鉛直上向き方向を y 方向と呼ぶ。

　　　  　　　

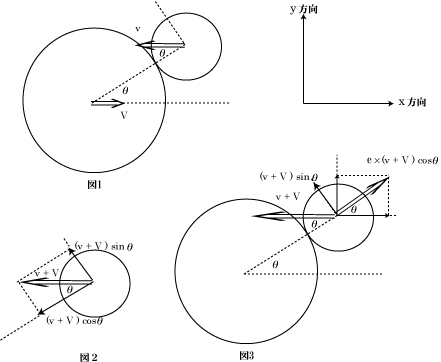
　図2 はバットの静止系でボールを見たものだ。バットに乗っかって考えると、ボールはバットに向かって速さ v + V で飛んでくるように見える。バットとの衝突面に垂直方向の速さの成分は、図の様に ( v + V ) cosθ となっている。一方、衝突面に沿った速さの成分は (v + V ) sinθ である：

　　　バットの静止系から見て、

　　　　　衝突直前の速さの衝突面に垂直な成分　　( v + V ) cosθ

　　　　　衝突直前の速さの衝突面に平行な成分　　( v + V ) sinθ

衝突面に垂直な方向の速さの成分は、衝突直後には、跳ね返り係数（反発係数）を e と書くと、e の割合で遅くなっている。もちろん 0 ≦ e ≦ 1だ。反発係数の定義は、衝突面に垂直な速度成分に対して

　　　　反発係数＝（衝突後の2物体の相対速度の大きさ）

　　　　　　　　　　　　　　　　　÷　　

　　　　　　　　　（衝突前の2物体の相対速度の大きさ）

と言える。だから、バットの静止系で見て、衝突直後の速さの衝突面に垂直な成分は、

e×( v + V )cosθ となる。衝突面に沿った、衝突面に平行な速度の成分は変わらない。

　　　バットの静止系から見て、

　　　　　衝突直後の速さの衝突面に垂直な成分　　e×( v + V ) cosθ　・・・（１）

　　　　　衝突直後の速さの衝突面に平行な成分　　( v + V ) sinθ　　 ・・・（２）

図3で、ボールから右斜め上方向に向かう2重矢印⇒が（１）、左斜め上を向いた矢印→が（２）だ。こうして、衝突直後にバットに対して持つボールの速さの水平方向の成分

v_x0^バットと、鉛直成分 v_y0^バット は、図3から

　　　　v_x0^バット= e ( v + V )cosθ×cosθ － ( v + V )sinθ×sinθ

　　　　v_y0^バット= e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ

と読み取れる。今度は、バットの静止系から私たちの居る本当の静止系に戻ろう。バットの静止系はバットとともに速さVで水平右向きに動いていたので、本当の静止系に戻すときには水平右向きの速度 V を加えればよい。私たちの静止系から見て、ボールはバットで打たれた直後、

　　　　v_x0= e ( v + V )cosθ×cosθ － ( v + V )sinθ×sinθ + V　　　・・・（３）

　　　　v_y0= e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ　　　　　　・・・（４）

という初速度でバットを離れるということだ。あとは、ニュートン方程式を解いて、飛距離を求めればよい。高等学校の物理の授業では「公式」を使って求める。大学に入って物理を専攻すると、1 回生ですぐに微分方程式としてのニュートン方程式を解いて求める。

　ニュートン方程式は

　　　　（質量）×（加速度）＝（力）

なので、ボールの質量を m [kg] 、水平方向の速度を v_x [m/s]、鉛直方向の速度をv_y [m/s]と書くと、水平の x 方向の運動方程式は

　　　m dv_x/dt = 0 　　　　・・・（５）

となる。ここで、dv_x/dt は v_x を時間 t で微分したもので、速度の時間変化が加速度なので、加速度の x 成分である。水平方向に力は働かないので、右辺は零だ。そうそう、空気抵抗は無視しておこう。

　鉛直方向には重力 mg が働く。ここで、g は重力加速度で、9.8 m/s²。下向きに力が働くので、負号に注意して、運動方程式は

　　　m dv_y/dt = －mg 　　　　・・・（６）

となる。（５）式は簡単で、v_x に時間変化が無いと言っているのだから、

　　　　v_x = （一定）＝ v_x0

だ。すなわち、水平方向には初速 v_x0 のまま、飛んでいく。ボールの位置 x の時間変化が水平方向のボールの速度 v_x になるので、位置 x は速さ(v_x) × 時間(t) なので、

　　　　x = v_x0 × t　　　　・・・（７）

でわかる。

　さて、鉛直方向の（６）式を解くと、

　　　　v_y = －gt + v_y0　・・・（８）

が得られる。実際に（８）を t で微分すると

　　　 dv_y/dt = －g 　　　　

が得られるが、これは（６）で両辺共通の m で割ったものに他ならない。また、（８）で時間 t = 0 の初期時刻では確かに初速 v_y0 になっている。鉛直方向のボールの位置 y を求めよう。位置 y の時間変化が速度 v_y であるので、

　　　　dy / dt = v_y

だから、右辺に（８）を代入して

　　　　dy / dt = －gt + v_y0　・・・（９）

これをyについて解くと（積分すると）

　　　　y = －g×t²  / 2 + v_y0×t　　・・・（１０）

が得られる。実際に t で微分したら（９）になることを確かめればよい。また、t = 0の、バットとボールが衝突した時間では、鉛直方向の高さを零とした。ボールの打点の位置を基準の高さ 0 と決めたということ。

　解いた答え（７）と（１０）から、ボールの飛距離がわかる。飛距離の位置を打点の高さ y = 0 としておこう。（１０）から y = 0 になる時間は、左辺の y に 0 を入れて

　　　　0 = (－gt / 2 + v_y0 ) t

とできるので、

　　　　t = 0  または　　t = 2×v_y0 / g

である。t = 0 は明らかに打った瞬間で、打点の高さは確かに 0 だが、飛距離を求めたいので、ボールが上がって落ちてくるまでの時間、t = 2×v_y0 / g を取る。この時間でボールは高く上がって落ちてくるが、その際、水平方向にはどれくらい飛んだかというと、（７）式だから

　　　　x = v_x0 × t = 2 v_x0 v_y0 / g

　　　　　= 2×[e ( v + V )cosθ×cosθ － ( v + V )sinθ×sinθ + V]

　　　　　　×[e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ]/ g

三角関数の公式を使ってちょっと整理しておくと

　x = [( v+V ) / g ] ×(1+e)×sin 2θ×[( v + V )×( e (cosθ)² －( sinθ)²  ) + V]　・・（１１）

が得られる。

　さぁ、数値を仮定して飛距離を見てみよう。もう一度確認だが、空気抵抗は無視している。プロ野球のボール、統一球というやつは、反発係数が 0.4034 から 0.4234 の間だそうだ。間を取って

　　　　e = 0.41

としておこう。ボールの速さは、時速 150 km とかだと、よう打たんので、時速 120 km  としてみる。それでも打ち返せないだろうなぁ。でもまぁ計算のため。

　　　　v_x0 = 120 km / 時 ≒　33.3 m/s

バットの長さは 106 cm 程度だそうだ。バットを持って体を回転させてバットのヘッドに速さVを持たせる。体の中心軸からバットを持つ手まで 40 cm 、バットの先から20 cm のところにボールが当たったとして、体の中心軸からおよそ r = 1.2 m のところにボールが当たったとする。バットを半回転、180 度回転するのに 0.2 秒でフルスイングしたとしよう。このとき、与えた角速度は ω=  π/0.2 rad/s。π は円周率で、角度をラジアンで測っている。そうしたら、バットの速さは

　　　　V = r×ω = 1.2×π/0.2 ≒　18.8 m / s ≒ 67.8 km / 時

時速 68 kmだ。重力加速度は g = 9.8 m/s² を使うので、（１１）式から飛距離 x [m] が、ボールがバットに当たった角度θの関数として求まる。数値計算の結果を描いてみよう。

　　　　　　　　

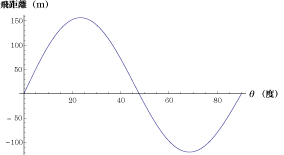
横軸が普通の単位、「度」で測った角度、縦軸が飛距離だ。角度 14 度で飛距離は 127 mとなり、角度 23.4 度のとき飛距離が最大で157 m になる。角度 33 度で再び飛距離は126 m 程度になる。フェンスの高さも考えないといけないが、14 度から 33 度でバットをボールに当てると、ホームランになりそうだ。角度 47 度を超えたあたりから飛距離がマイナスになるが、まぁ、キャッチャーのファウルフライというところだろうか。

　お題は、「ホームランが打ちたい」だった。普通にやっていては打てない（かもしれない）から、なんとか打とうという企画であった。とりあえず、反発係数の大きな場合を考えてみよう。スーパーボールを落下させて、床面に衝突したあと、最初の高さの 80 % 位まで戻ってきたという実験があるそうだ。高さ h [m] から落とすと、エネルギー保存則を使うと、床面に衝突する直前の速さは √(2gh) となることがわかり、この後  0.8 h の高さまで上昇するので、衝突直後の速さは √(2g×0.8h) となるので、反発係数は

　　　　√(2g×0.8h) / √(2gh) ≒ 0.89

で、およそ 0.9 だ。スーパーボールでホームランを狙おう。

　反発係数を 0.9 にして計算し直して見る。

　　　　　　　

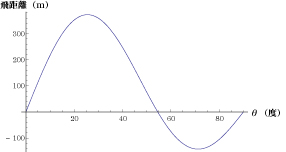
今度は、角度 6 度で飛距離は 136 m、角度 25.8 度で最大の飛距離 373 m がでる。角度47 度で 129 m まで落ちるが、120 m を超えているので、十分ホームランだ。当たる角度が少々悪くてもホームランが狙える。

　時速 120 km のボールを打つのは難しいし、フルスイングしてもバットの速度が速くならないかもしれない。空気抵抗もあるだろう。

　だけど、今までの条件で飛距離が最大 373 m 出るんだから、条件を緩めても、きっとホームランは打てる、よ。

　と、願っておこう。

５２．集合

　小学生の時、算数の授業に「集合」が取り入れられた。取り入れられて間もない頃だったと思う。「AまたはB」とか「AかつB」とかあって、ベン図なんてものを習った。小学生にも小学校の先生にも、なんで小学生に集合論と思ったことだろう。

　今から考えるに、思いっきり、ニコラ・ブルバキの影響だったんだと思われる。

　ニコラ・ブルバキ。フランスの幾人かからなる数学者集団で、数学を基礎から再構成しようとしていたようだ。最も基礎に置いたのが「集合論」だったと思う。大学生になって生協の本屋にブルバキの本がずらりと並んでいた。どうせ読まないだろうが、あまりに壮観なので一寸欲しかったが、物理を専門にするつもりだったので、そこまで手が回らなかった。

　「数」をどうやって基礎づけるか。数学者というのは、当たり前のように思えることまで考える人たちだ。大学時代、学科が分かれていなかったので語学の授業で「クラス」のようなものが出来上がっていたのだが、そのおかげで物理だけではなく、化学志望や数学志望の友人などができた。数学志望の友人から、「１」「２」「・・・」と、数の概念を把握するのは実は難しいことなんだと聞かされていた。リンゴが1個、ミカンが1個、人が一人、具体的に違うのに、「１」という共通項があることを理解するのは難しいことだと言っていた。当時は何のことかよくわからなかったが、リンゴが1個、ミカンが1個、人が一人、全部抽象化したときの「1」を、どうやって、リンゴとかの個別、実態に頼らずに「１」を導入するか、ということを、数学の解っていない物理志望のやつに言いたかったのかもしれない。

　そこで、どうやら、集合論が必要になるようだ。数学者じゃないし、勉強してないから間違っているかもしれないが。

　「りんごが1個ある集合」とか、「人がひとり居る集合」とか考えて、その要素の数が「１」と言ってもダメならしい。要素に個性がある。抽象化されていない。

　そこで、「要素が何もない集合」というのを考える。「空集合」だ。記号では∅。具体的に何も入ってないんだから、リンゴでもミカンでも人でもない。具体的でないんだから抽象的だ。「何もない」。そこで、空集合に「０」を対応させる。

　次は、1。要素が一つの集合を考えたいが、リンゴとかの具体はダメ。そこで、「空集合を要素に持つ集合」を考える。考えている集合の要素はただ“一つ”。その要素がまた集合で、それが「空集合」。集合の集合を考えるわけだ。集合の要素を中括弧　{　}の中に書くと、{∅}という集合だ。「空集合を要素に持つ（集合の）集合」を考え、これに「１」を対応させる。

　2 はどう定義するか。具体的でない要素を“2つ”持たせる。空集合φと、空集合を要素に持つ集合{∅}を考え、これらの集合を要素に持つ（集合の）集合を考える。要素を書けば{∅, {∅} }ということだ。具体でない抽象的な要素を持つこの集合に「２」を対応させる。

　あとは、同じ。「３」は今まで導入した集合を要素に持つ集合{∅, {∅}, { ∅, {∅} } }を考えて、「３」を定義する。

　以下、順々にして、0を含む自然数は定義できる。

　数学者というのはややこしいことを考えるものだ。おかげで、小学生から集合を学ぶことになった。

５１．原子核のアルファ・クラスター

　水素からはじまって、ヘリウム、リチウムと、原子核に含まれる陽子の個数が増えていくにつれ、特有の元素として元素記号が与えられている。普通の水素原子核は陽子が1つからできていて、元素記号は H。ヘリウム原子核は陽子 2 つと中性子 2 つからできているものが多く、元素記号は He。陽子 2 つ、中性子 1 つからなるヘリウム原子核もあり、これはヘリウム 3（³He）と呼んでいる。普通の奴は、ヘリウム 4（⁴He）。原子核に含まれる陽子の個数を原子番号と呼び、原子核に含まれる陽子と中性子の個数を足した数を質量数と呼ぶ。質量数を元素記号の左上に記す。元素の種類は原子番号で決まる。

　原子核ではヘリウム 4 は極めて安定で、ヘリウム 4 を纏まりとして、原子核を考えることもできる。例えば、安定な炭素 12 の原子核は陽子 6 個と中性子 6 個からなるが、ヘリウム 4 が 3 個からなると考えても良い状態がある。また、安定な酸素 16 の原子核は陽子 8 個と中性子 8 個からできているが、ヘリウム 4 が 4 個からできているとした方が理解できる状態もある。

　ヘリウム 4 の原子核は安定なのだが、陽子の個数が一つ増えたリチウム 5（⁵Li）とか、中性子の数が一つ多いヘリウム 5（⁵He）は、原子核としては極めて不安定である。そうすると、宇宙ができた直後とか、恒星の内部で、軽い原子核から順々に重い原子核を作ろうとしても、“5”のところで行き詰まる。リチウム 5 とかヘリウム 5 とかができてもすぐに壊れてヘリウ ム 4 と陽子、または中性子に戻ってしまい、ヘリウム 4 より重い原子核ができないことになってしまう。

　そこで、ヘリウム４原子核は安定なのだから、これが 2 つぶつかって融合してベリリウム 8（⁸Be）という原子核になれば良いと考えたくなる。ところが、陽子と中性子をあわせて 8 個持つ原子核もおしなべて不安定である。ベリリウム 8 も、できてもすぐに壊れる。寿命が極めて短い。大学 3 回生のときにグループに分かれて半年かけて行う課題実験で、タンデム・バンデグラフ加速器なるものを使ってベリリウム 8 の寿命と偶奇性を測定する実験というのを行った。結果は、ベリリウム 8 が存在しても寿命は10^－22秒程度という結論だった。この世で最も早い光が原子核一つの端から端まで進む時間がおよそ10^－23秒程度。相互作用がベリリウム 8 の端から端まで伝わる程度で原子核が壊れてしまうのだから、到底存在するとは言えない。

　では、原子核はヘリウム 4 までしかできないのか。私たちは水やらタンパク質でできているが、それらの構成要素としては、原子番号 6 の炭素（C）や、原子番号 8 の酸素（O）が多量に存在している。私たちが存在するのだから、原子核の陽子・中性子の個数の和である“質量数”が5以上の原子核が出来てくれなくては困る。

　そこで、フレッド・ホイルという人が、ヘリウム 4 が二つ衝突して極めて短時間だがベリリウム 8 の状態になり、それが壊れて 2 つのヘリウム 4 になる前にもう一つヘリウム 4 が衝突して炭素 12（¹²C）ができると考え、炭素 12 の原子核にはヘリウム 4 が 3つに対応したえエネルギーのところに共鳴状態があると提唱した。これは「ホイル状態」と名付けられたが、実験的に実際に見つかる。こうして、恒星の中でヘリウム 4 から炭素 12 が作られる道が見つかり、あとはヘリウム 4 を順次くっつけて、酸素16（¹⁶O）、ネオン 20（²⁰Ne）、マグネシウム 24（²⁴Mg）、けい素 28（²⁸Si）などなど、重い原子核、つまりは重い元素が合成されていくことが理解された。

　ちなみに、フレッド・ホイルは、ガモフが大爆発で宇宙が出来たと提唱した時、ちょっと蔑ずんで、その大爆発のことを「ビッグ・バン」と呼んだ人だ。

　大学院生のとき、炭素 12 は安定なのに、ベリリウム 8 は何で安定でないんだろうと思っていた。あまり正しくはないかもしれないが、炭素 12 もヘリウム 4 が 3 つから出来ていると仮に考えると、簡単な理屈がある。

　ヘリウム 4 の原子核、いちいち面倒くさくなってきたので、歴史的な経緯からヘリウム 4 の原子核のことを「アルファ粒子」と呼ぶことにするが、2 つのアルファ粒子に引力が働くと考える。この引力による 2 つのアルファ粒子間の位置エネルギーを－Vとする。マイナス記号を付けたのは引力でエネルギーが得をするから。アルファ粒子の運動エネルギーを T と書くと、アルファ粒子は 2 つあるので、ベリリウム 8 の運動エネルギーは T + T = 2T と、2 倍の T だ。しかし、ベリリウム原子核のことだけを考えるのならば、ベリリウム原子核は静止していると考えた方がよい。これは、ベリリウム原子核の重心運動を分離して、重心運動の運動エネルギーを別に考えるということだ。正確にいうと、2 つのアルファ粒子からなる系を重心運動と相対運動に分けるということ。その上で、重心は静止しているとしたらよい。重心と言ってきたが、正確を期すと、「慣性中心」。ベリリウム 8 原子核の運動エネルギー  2T のうち、T が重心の運動エネルギーになる。こうして、重心運動を除いて、「静止」したベリリウム 8 原子核の全エネルギー（= 運動エネルギー + 位置エネルギー ) は

　　　　T + (－V ) =　 T － V

となる。しかし、ベリリウム 8 の原子核は安定に存在しないので、このエネルギーは正または 0 のはずだ。安定だったら引力で束縛されていて、全体のエネルギーが負になっているはずだから。まぁ、きわめて短時間はベリリウム 8 が存在すると考えて、カツカツ 0 と考えておこう：

　　　　T － V ≒ 0　　　・・・（１）

　では、炭素 12 ではどうだろうか。アルファ粒子が 3 つからなると考えると、3 つのアルファ粒子の運動エネルギーは、T + T + T = 3 T 。ただし、このうち、重心運動の運動エネルギー T を除くと、3 つのアルファ粒子の相対的な運動のエネルギーは、3 T － T = 2 Tとなる。では、アルファ粒子間の位置エネルギーはどうなっているか。3 つのアルファ粒子に、1、2、3と名前を付けると、1-2 間の相互作用の位置エネルギー（－V）と、2-3 間の相互作用の位置エネルギー（－V）と、3-1 間の相互作用の位置エネルギー（－V）と 3 つ出てくるので、（－V）+（－V）+（－V）= －3 V となる。こうして、炭素 12 原子核の全エネルギーは

　　　2 T + （－3 V ）= 2 ×( T － V ）－ V

　　　　　　　　　　　≒ － V

となる。ここで、ベリリウム 8 で成り立つ事実（１）式を用いた。こうして、炭素 12原子核の全エネルギーは －V < 0 と負になるので、2 つのアルファ粒子からなるベリリウム 8 原子核は不安定で存在しなくても、3 つのアルファ粒子からなる（と仮定した）炭素 12 原子核は束縛状態として存在することがわかる。

　2016 年に、陽子が 113 個ある原子核に名前が付いた。ニホニウム（Nh）と、日本に関係する名称がついた。2004年当時、埼玉和光の理化学研究所にいた森田浩介さん率いるグループが、2004年7月23日に、亜鉛 30 とビスマス 83 の原子核をぶつけて初めて113 番元素を作った。2004年秋、9月27日から30日まで行われた日本物理学会秋季大会の申し込みには間に合わなかったので、急遽追加公演として突っ込んだ。その時、高知大学で行われた物理学会の実行委員をしていたので、学会の何日目か、確か 3 日目だったと思うが、当時、大学で一番収容人数の多い教室であった 210 番教室で行われていたセッションの最後に、追加で森田さんに 113 番元素の発見の講演をして頂いたことを覚えている。113 番元素発見の第一報は高知発であった。その、ニホニウムは 0.002秒でアルファ粒子（α）を 3 個出して壊れる。

　　　　²⁷⁸Nh　→　²⁶⁶Bh　＋　3α

または、6 個のアルファ粒子を出して壊れる。

　　　　²⁷⁸Nh　→　²⁵⁴Md　＋　6α

どちらにしても 1000 分の 2 秒の寿命、2×10^－3 秒の寿命というのは、ベリリウム 8 に比べてはるかに長い。

　日本初の元素の誕生に、ほんの微かに、学会発表の教室のアレンジというだけではあるが関われて、high intelligence の誉れである。

５０．スーパーボールの衝突

　スーパーボールなる、子供が喜ぶ小さいボールが売られている。なにがスーパーかというと、良く跳ねること。アスファルトなんかに叩きつけると、勢いよく跳ね返る。昔、子供の時分には値段はそこそこ高かったので一つ二つくらいしか持っていなかったが、今では100円ショップで大きさも色も、とりどりのスーパーボールがいくつも入って100円＋消費税で売られている。

　授業で、物体の衝突の問題を扱う際に、面白い実例を見せようと思って、スーパーボールと厚紙で図のようなものを作ったことがある。

 　　　　　　　　　　　　　　

　大きい方のスーパーボールに、紙で作った円筒をどうにかして貼っておく。その円筒の中に、できれば円筒にぴったりの別のスーパーボールを入れておく。円筒を持って、自由落下させる。そうすると、全体が床に当たって跳ね返った時に、円筒の中に入れたスーパーボールが勢いよく飛び出してくる。

　実演してから、計算を、と思ったが、実際に落としてみると、かなりの勢いでスーパーボールが飛び出してくることがわかった。しかも、正確にまっすぐに落とさないと、円筒がまっすぐに上を向かず、少し横に向いたら、向いた方向に目がけて中のスーパーボールが結構な速さで飛び出してくるので、飛び出した方向に人が居たら、かなり危ない。安全性が確保できないので、授業で演示するのは断念。

　学生さんにしてもらおうとした計算だけ記しておこう。

　物体が衝突したら、普通、エネルギーは失われる。熱になったり、音が生じたり。しかし、スーパーボールは良く跳ねるので、エネルギーは失われずに跳ね返ると仮定しよう。言葉で言えば、「完全弾性衝突」だ。２つのスーパーボールの衝突の前後で、運動量と力学的エネルギーは変化しない。これを頼りに考えてみる。

　　

　図の左端のように２つのスーパーボールは地面に向かって同じ速さで落下してくる。下の大きくて重い方のスーパーボールの質量を m₁ [kg]、円筒の中に入っている、上の小さくて軽い方のスーパーボールの質量を m₂ [kg] としておこう。下のボールが地面にぶつかって跳ね上がる。エネルギーを失わずに跳ね返って跳ね上がるとしたので、地面に当たる直前の下側のボールの下向きの速さを v [m / s] としておくと、地面に衝突直後は下のボールは上向きに速さ v [m / s] となっている。そこへ、上側の軽いスーパーボールがやってくる。図の真ん中の状況だ。お互い、速さ v [m / s] で正面衝突する。上向きを正の方向とすると、下向きの速さは －v [m/s]とマイナス符号（負号）を付けておけばよい。このとき、2つのスーパーボールの衝突後（右端の図）の運動量は、衝突前（図の真ん中）の運動量と同じである。運動量は、（質量）×（速度）なので、

　　　　m₁ v － m₂ v ＝ m₁ v₁ ＋ m₂ v₂　　　・・・（１）

が満たされる。衝突の前（左辺）と後（右辺）で運動量の総量は変化していないという式だ。また、衝突の前後で物体の位置エネルギーは変化しないので、運動エネルギーだけ考えて、衝突の前後で運動エネルギーが変化しないとすると

　　　　　m₁ v² / 2 + m₂ v² / 2 ＝ m₁ v₁² / 2 ＋ m₂ v₂² / 2　　・・・（２）

となる。それぞれの運動エネルギーは、　( 1 / 2 )×（質量）×（速度の2乗）。（１）式と（２）式を連立方程式として解いて v₁ と v₂をもとの速さ v で表すと、

　　　　v₁ = ( m₁ － 3 m₂ ) / (m₁ + m₂ )× v

　　　　v₂ = ( 3 m₁ － m₂ ) / (m₁ + m₂ )× v 　・・・（３）

と得られる。

　さて、下側のスーパーボールは上側のスーパーボールより重いとした。そこで、m₁ は十分 m₂ より大きいとして、得られた（３）式で、m₁ に比べて m₂ を無視してしまおう。そうすると

　　　　v₁ ≒ v

　　　　v₂ ≒ 3 v 　・・・（３）

となることがわかる。速さ v₂ は上側のスーパーボールの速さなので、地面に衝突する前の 3 倍の速さを持って跳ね上がることがわかる。

　実際にやってみると、本当に勢いよく飛びあがるので、面白いが、危ない。

　今はきちんと計算してから、下のボールが上のボールより圧倒的に重いと近似した。ちょっとサボって、下のボールは上のボールより圧倒的に重いので、図の真ん中の状況で、下のボールは上のボールが衝突してきても何ら影響されないとしてみよう。下のボールから見ると、上のボールは相対的に速さ 2v で近づいてくる。衝突後は、速さ 2v で下のボールから遠ざかるだろう。下のボールは衝突後も影響されないとしたので、上向きに速さ v で動いている。このボールに対して上のボールは速さ 2v で上向きに動いているのだから、静止している私達から見ると、上のスーパーボールは上向きに速さ 3v で動いているはずだ。きちんと計算してから近似して得られた（３）の結果と同じだ。

　今度は、さらに軽いスーパーボールを載せて 3 段重ねにする。2 段目のスーパーボールの速さ 3 v と 3段目のスーパーボールの速さ －v の速度を持った 2 球の衝突になるが、2 段目のスーパーボールの重さより 3 段目のスーパーボールの重さが圧倒的に軽いとすると、今度は 2 段目のスーパーボールから見て 3 段目のスーパーボールは相対的に速さ 3v － (－v) = 4v で衝突してくる。2 段目のボールは重くて 3 段目のボールが衝突してきても何ら影響されず、相変わらず上向きに 3v の速さで動いているとしよう。3 段目のボールは衝突後、2 段目のボールに対して速さ 4v を維持して上向きに離れていくだろうから、2 段目のボールの上向きの速さ 3v に対して、4v の速さで 3 段目のスーパーボールは上向きに跳んでいく。つまり、静止している私達から見て、3 段目のスーパーボールは近似的に速さ 7v （＝4v + 3v ）で飛び上がっていくはずということだ。

　計算上、スーパーボールをどんどん積み重ねておいてから落とすと、一番上のスーパーボールの速さは相当なものになるはずだ。恐ろしい、危険だ。

４９．長さ・重さ・時間の単位

　光速度の測定の歴史に48回で触れたが、現在ではレーザー光を使って極めて精度よく光速度が測定されている。

　特殊相対性理論を構築する際に実験事実として置かれる光速度不変の原理、つまり、すべての慣性系の人にとって真空中では光の速さは同じ値を取る、という事実、要するに、ある慣性系に静止している観測者に対して一定の速度で運動している別の観測者に対しても真空中では光の速さは同じ値を取る、という事実と、光速度があまりに精度よく測定されていることで、今や、光速は「定義値」となっている。普通の「長さ」や「時間」を使って、光の速さ c は

　　　　c = 299792458 m/s

なのだが、真空中の光の速さが慣性系の誰にとっても同じであることを逆手にとって、現在では光の速さから逆に「長さ」の単位を決めるようになっている。

　今はMKS単位系という単位系に基づいて、講義を行っている。Mは長さの基本単位メートル、Kは質量（重さ）の基本単位kg、Sは時間の基本単位s(econd)（秒）ということだ。電磁気学を扱うには、これに加えて電流の基本単位アンペア(A)を加え、MKSA単位系と言われるが、ここでは電磁気はやめておこう。

　私が学生の頃は、cgs 単位系（センチメートル(cm)、グラム(g)、秒(s))の単位系が多く使われていて、電磁気学に至っては、ガウス単位系とか色々錯綜しており、勉強するときにかなり厄介であった。教科書によって、使っている単位系が違うので、方程式に出てくる係数が異なっていた。

　さて、長さと重さと時間を見ておこう。

　18世紀ころまで、世界中で統一された長さの単位は存在していなかった。18世紀まで世界中というよりは、ごく限られた地域でも共通の長さの単位はなかなか決められない。そこで、18世紀末のフランスで、長さの単位を決めるプロジェクトが始動する。ルイ16世の治世の時であった。1789年にバスチーユ牢獄襲撃に端を発してフランス革命が起き始める。革命の精神は「自由・平等・博愛(Liberté, Égalité, Fraternité）」である。そこで、地域、人種、民族等々に関わらず平等に長さの単位を決めようとして、地球を基準にすることに決める。

　　　　北極から赤道までの距離の1000万分の1を「1メートル」と定める

実際にはフランス北部のダンケルクからパリを通る子午線に沿って、スペインのバルセロナまで測量を行い距離を測り、極から赤道までの長さを割り出して、1メートル（1 m ）を決定した。1792年に測量を開始し、1 mが決まった時には、命令を出した国王ルイ16世はすでに断頭台に消えていた。

　長さの単位1mが決まったので、重さは、

　　　　1辺が10cm （＝0.1 m)の立方体（1000 cm³)の水の重さを単位にとり、

　　　　これを 1 kg の質量と定める

　さらに、時間は地球の1自転を1日と定め、1日は10時間、1時間は100分、1分は100秒、10日で1週間と定めたが、これはフランス人にも不評だったようで、革命後、やまっている。10進法が便利だが、慣れ親しんだ24時間、60分、60秒が使われる。革命政府の時間だと、1日は100000秒、いつも使っている時間だと、1日は86400秒。革命政府の1秒は今の0.864秒。

　先に時間の単位の定義を見ておこう。

　1960年に、「1秒」が再定義されている。1900年という特定の1年を取り、この

　　　　1900年の1年間の長さの31556925.9747分の1を「1秒」

と定義した。ちなみに31556925.9747=60（秒）×60（分）×24（時間）×365.2421988（日）である。

　その後、1967年からは、

　　　　『セシウム133原子の基底状態の2つの超微細準位間の遷移に対応する放射の周

　　　　　期の9192631770（91億9263万1770）倍に等しい』　　　　・・・（１）

として、1 秒 が定められ、現在に至っている。セシウム133 原子のエネルギーの最も低い状態は微妙に 2 つに分かれており、高いエネルギー準位から低い方へ電子が遷移すると光を放出する。光は波なので振動しているが、その振動回数が 9192631770 回続いた時の時間間隔を 1 秒と定めている。ただし、1997年にこのときのセシウム原子は絶対 0度に置かれているという条件が加えられている。

　ちなみに、6 週間は何秒になるだろうか。1 秒が 60 集まって、1 分、それが 60 集まって 1 時間、それが 24 集まって 1 日、それが 7 集まって 1 週間、それが 6 集まって 6週間と考えていくと、

　　　　　1×60×60×24×7×6

　　　　＝1×(2×3×10）×(3×4×5)×(3×8)×7×6

ここで、下線を付けた 3 どうし掛けると 3×3＝9 だから、

　　　　　1×60×60×24×7×6

　　　　＝1×2×10×3×4×5×9×8×7×6

　　　　= 1×2×3×4×5×6×7×8×9×10

　　　　= 10 !

と、1 から 10 まで掛けた数、10 の階乗(10 ! )秒になっている。びっくりしたからビックリマーク（ ! ）を付けた訳ではない。

　だからどうなんだ。まぁ、こんな話をしているのではなかった。

　さて、長さの単位の定義に戻ろう。1792年にフランスで 1 mが決められた。それを基に、1889年には、

　　　　ある特定のプラチナ・イリジウム合金の棒を氷が融ける温度の環境に

　　　　置いたとき、その棒上に刻んだ2本の線の間の距離

を 1 mと定めなおした。いわゆる「メートル原器」である。1960 年になるとさらに定義が変えられる。

　　　　クリプトン86原子が真空で放射する電磁気（光）スペクトルのオレンジ・

　　　　赤の輝線の波長の1650763.73（165万763.73）倍

を 1 m とした。

　最終的に、光速度不変の原理を基にして、光の速さは「定義値」とし、1 m は

　　『光が真空中を299792458分の1（2億9979万2458分の1）秒かけて移動する距離』

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・（２）

とされ、現在に至っている。長さを決めるのに時間の定義を必要としている。

　（１）と（２）で時間と長さが決まった。次は重さだ。1000立方センチメートルの水の重さではなく、1889年に、

　　　『プラチナにイリジウムを10％混ぜた合金で作られたキログラム原器』　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・（３）

の質量を 1 kg と定め、現在に至っている。各国にキログラム原器のコピーがあって、それを標準としている。質量だけなんかアナログ感がある。

　しかし、質量の定義はもうすぐ変更される予定だそうだ。

　フランスに留学するとき、長さの単位がメートルでなくてフィートとかだったら嫌だなぁと思っていたが、メートルの発祥はフランスなのだから、無知なる危惧であった。

　そういえば、私が子供の頃には、まだ家に「鯨尺」なる物差しがあり、寸や尺の目盛りが刻まれていた。

４８．光速は、なぜか c

　46回、47回と、光の速さの話題が続いた。光速には c という文字を使うことが習わしだが、何故なのだろう。授業では、力は英語で force だから、F と書いて、質量は massだから m と書いて、加速度は acceleration だから a と書いて、ニュートンの第 2 法則は

　　　　F = m a

だよね、とか話すが、さて、光速 c。

　光速の英語、speed of light のどこにも c が無いぞ？　ラテン語で光は lux。ギリシャ語だと φωζ (fos)。ラテン語で速さは volo。英語では velocity なので、速度は v で表すことが多い。困ったぞ。ただ、ラテン語で速さは celeritas というのがあるので、この cかもと思ったが、光はどこへ。光速だと、 celeritas lucis か。

　どうやら、19世紀の電磁気学の発展に鍵があるようだ。

　静止した2つの荷電粒子（電荷をもった粒子）に働く力は、クーロンの法則として知られている（1785年）。力 F は、2つの粒子の電荷をそれぞれ q、Q とし、2 つの荷電粒子間の距離を r とすると

　　　　F = k qQ / r²　　・・・（１）

となる。k は比例定数。

　荷電粒子が運動していると、2つの荷電粒子間に働く力は、（１）式に加えて、速度dr/dt、加速度 d²r/dt² に依存した補正が加わる。ウェーバー (W.Weber, 1804－891）は速度に依存した（１）式の補正項を

　　　　－qQ / r² ×（1 / c² )×（dr / dt)²

とおいた (k=1とした）。ここに、定数 c が現れた。この c は「定数：constant」の c から採用されたようだ。

　ウェーバーはコールラウシュ(R.Kohlrausch, 1809-1858)とともに、2 つの運動する荷電粒子間の力に現れる定数 c の測定実験を行い、

　　　　c = 4.39×10⁸ m/s

という値を得ている（1856年）。光速 3.0×10⁸ m/s に近い定数であることに気づいていたらしいが、それ以上は突っ込んでいないようだ。

　実は、ウェーバーの補正項に現れる c は光速と関係があった。ウェーバーの c を c_w と書いて、本当の光速を c と書くと、両者には

　　　　c_w= √2× c 　　（c_w² =2 c² )

の関係があった。光速 c にルート 2 = 1.41421356・・・（一夜（ひとよ）一夜に人見ごろ・・・）を掛けると、4.24×10⁸ m/s となり、近い測定値である。

　こうして、√２だけ違ったが、今も光速度にウェーバー・コールラウシュの c が使われているのではないのだろうか。そうであれば、定数、constant の c ということで、光にも速度にも関係ない文字なのだが。

　そういえば、研究室に、コールラウシュの Praktische Physik （実験物理学）の和訳本がある。第 3 巻を持っていないのではあるが。もともとの Kohlrausch のPraktische Physik の初版は1870年だ。ウェーバー・コールラウシュと時代が合わないぞと思っていたら、「実験物理学」の著者のコールラウシュは F. Kohlrausch （1840－1910）だった。その父がウェーバーと実験を行ったR. Kohlraussch。

４７．光速の測定

　46回の、光の粒子説と波動説の話（粒子性と波動性ではない）のところで、水中での光の速さが空気中の光の速さよりも遅ければ、光の波動説に軍配が上がりそうなことを見た。

　そもそも、光の速さはどうやって測ってきたのだろうか。

　まずは、17世紀のガリレオ・ガリレイ(1564-1642)。ガリレオは正しく、光の伝わる速さは有限であると認識し、その速さを測定しようとした。離れた2点に人を立たせ、箱の中にろうそくを立てたものをそれぞれの人が持つ。初めに、こちらの人が箱の覆いを開けて向こうの人にろうそくの火を見せる。向こうにいる人は、こちらの人が覆いを取った t₁ 秒後に明かりを見て、明かりを見たら直ちに自分の箱の覆いを開けてこちらの人にろうそくの明かりを示す。こちらの人は、自分が最初に覆いを開けてから t 秒後に相手の光を目にする。この時間から光の速さを割り出そうとした。二人の距離を L [m] とすると、光速 c [m/s] は

　　　　c = 2L / t

で求められるはず。しかしながら、　もちろん、光の速さが速すぎて、測定ならず。1638年の記述である。

　17世紀半ば、1676年頃、レーマー(O.C.Romer, 1644-1710)は、木星の衛星イオの公転周期が見かけ上変化していることを観測で明らかにする。木星の陰からイオが顔を出した瞬間の時刻を t₁ [s] とし、イオが木星の前を通って裏側に消え、再び姿を現す時刻を t₂ [s] とする。そうすると、イオの公転周期 T [s] は、T = t₁－t₂ となる。ところが、地球と木星の距離は変化しているので、最初にイオが顔を出した時刻での木星と地球の距離を d₁ [m]、次に姿を現した時の木星と地球の距離を d₂ [m] とすると、光の速さ c [m/s] で情報が伝わってくるので、地球から見て、イオが最初に顔を出した時刻は地球上では t₁’ [s] となり、、次に姿を現した時刻は地球上では t₂’ とすると

　　　t₁’ = t₁ + d₁ / c , 　　　　t₂’ = t₂ + d₂ / c

となるはずだ。地球と木星との距離の変化は、地球と木星の相対的な速さを v [m/s] とすると、速さ×時間で動いた距離 d₂―d₁ になるはずなので、

　　　　d₂―d₁ = v T

となっているはずだ。こうして、イオが木星の端から顔を出してから木星の周りを1周回って次に姿を現すまでに地球で観測した時間 T’ は

　　　　T’ = t₂’ － t₁’

　　　　　= t₂  － t₁ + ( d₂－ d_{1 )} / c

　　　　　= T + v T / c

　　　　　= T ( 1 + v /c )　　　　　　　　・・・（１）

となる。レーマーは丹念に木星のイオの公転周期 T’ の変化を観測し、データを残した。そのデータに基づき、上の式から光速 c を導いたのは、オランダのホイヘンスであった。観測データから v=0 の時を見つけ、真の公転周期 T を見つける。また、v が分かれば、c が分かる。こうして、データを分析して光速 c が求められた。結果は、2.3×10⁸ m/s であり、現在の値（近似的には3.0×10⁸ m/s）とは、ずれているが、桁の10⁸ は合っているのは大したものだ。

　18世紀、1728年になるとブラッドレー(J.Bradley, 1693-1762)は恒星の光行差の観測を行う。真上から雨が降ってきても、人が歩いていると、その人には斜め前方から降ってくるように感じられる。それと同じように、遠方の恒星からの光は、地球が動いていることで、本来の角度からずれてやってくるように感じられる。

　　　

　話を簡単にするため、地球から見て天頂に恒星が位置しているとしよう。真上から雨が降るように、まっすぐ真上から恒星の光はやってくるが、地球が動いているために斜めから光が来るように見える。恒星からやって来る光が天頂となす角度を θ [rad] として、天頂の恒星から地球までに光が届いた時間を t [s] とすると、上の右図のような配置になる。地球の速さは v [m/s] とした。そうすると、三角法を使って

　　　　sin θ= ( vt ) / ( ct ) = v / c 　・・・（２）

となるので、光行差 θ を観測し、地球の速さ v = 2πr / T から、（２）式を使って光速 c が分かるという寸法である。ここで、r は地球と太陽の距離、1億5000万km、T は地球の公転周期 1 年である。

　地上で光速を測定したのは、フィゾー(H.Fizeau, 181901896)であった。19世紀半ば(1849年7月)のことである。回転する歯車を使う。歯車の歯の個数を n 個、1秒当たり歯車は N 回転するとしよう。回転する歯車の歯の隙間を狙って光を発する。その光がうまく歯の間をすり抜けて、距離 L [m] 離れたところに置かれた鏡で反射して、戻ってくる。また歯車のところまで来るが、歯車は回っているので、次の歯のところにきていたら、戻ってきた光はそこでさえぎられる。丁度、1/(nN) [s] 経ってから光が戻ってくると、歯に邪魔されず、次の歯の隙間を通って光は戻ってくる。こうして、光速を c [m/s] として、速さ×時間で進んだ距離なので

　　　　c × (1/(nN)) = 2L 　・・・（３）

が得られる。光が往復するので、光が進んだ距離は右辺の 2L となる。こうして、初めてフィゾーが地上で光速を測定した。3.15×10⁸ m/s という速さを得たらしい。

　もともと、フィゾーは、パリ天文台のアラゴ(D.F.J.Arago, 1786-1853)の計画をもとに、フーコー(J.B.L.Foucault, 1819-1868)と光速測定の実験をしていた。フィゾーの友人フーコーは、フーコーの振り子のフーコーである。4年間共同実験を行っていたが、異なるアイデアを持っていたらしく別々に実験するようになり、それぞれ単独で光速測定を計画した。フィゾーは前述の回転する歯車を用いたが、フーコーは回転する鏡を用いて光速を測定しようとした。先にフィゾーが空気中での光速を地上で測定したとき、それには 8600 メートル以上離れた 2 地点間での実験を要した。フーコーはテーブルトップ、4メートル程度の装置で光速を測定しようとする。

　　　　　　　　

　図のように、光源から回転する鏡、回転鏡に向かって光を発する。この光が回転鏡M₁で反射し、回転鏡を取り囲むように設置されている球面鏡 M₂で 反射する。M₁ と M₂の距離を L₁ [m] としよう。光がここを往復する時間 t [s] は、

　　　　t = 2L₁ / c

だ。往復だから、L₁ の2倍。光が球面鏡で反射されて回転鏡に戻ってきたとき、回転鏡は少し回転している。回転鏡の回転の角速度を ω [rad/s] とする。すると、光が2つの鏡の間を往復した時間 t のあいだに、回転鏡は角度

　　　　Δθ=ωt = 2L₁ ω/ c

だけ回転している。球面鏡から戻った光は、少し回転した鏡 M₁で再び反射される。回転していなかったときには光は来た道を帰るが、鏡が Δθ [rad] だけ回転しているので、すこしずれて反射され、図の点線の道をたどる。どれだけずれるかというと、回転鏡に入射するときに入射角が Δθ [rad] ずれていて、反射の法則から反射角と入射角は同じだから、反射する際にも反射角が Δθ [rad] ずれる。あわせて 2×Δθ [rad] ずれて戻っていく。光源にまで戻ると明るくて見えないので、途中で半透明の鏡を置いておいて、図のようにスクリーンに誘導する。回転鏡が回転しなかったときには光はスクリーン上のA点に来るはずだが、回転しているのでB点にやってくる。そのずれ Δx [m]は、回転鏡からB点までの距離を L₂ [m] とすると、

　　　　Δx = L₂ ×2×Δθ

　　　　　　= 4 L₁ L₂ ω / c 　　・・・（４）

と得られる。こうして、回転鏡が回転していないときと回転しているときでのスクリーン上に来る光の位置のずれ Δx [m] を測定すると、（４）式から、光の速さ c [m/s] が測定される。

　フーコーは毎秒8000回転する回転鏡で、2.98×10⁸ m/s という光速の値を得た。かなり正確である。

　また、回転鏡と球面鏡の間に水で満たした管を置いて、そこを光が通るようにし、水中での光の速さは空気中での光の速さからどれだけずれるかを調べた。そうして、水中の方が空気中より光の速さは遅いことを示し、46回で述べた光の波動説の正しさを示した（粒子説では水中の方が空気中より光速は速いはずだった）。友人のフィゾーはその7週間後に自身の実験でフーコーと同じ結論を得ている。

　パリ天文台のアラゴは両人の結果を喜んだそうだ。

　　　　

　パリに住んでいたとき、パリ天文台のそばのアパルトマンを借りて暮らしていた。モンパルナス大通り（Boulevard Montparnasse）とラスパイユ大通り（Boulevard Raspail）に挟まれた区画であったが、天文台が近くにあったので、少し行けば「アラゴ大通り（Boulevard Arago）」があった。シャルルドゴール空港からモンパルナスまでエールフランスの空港連絡バスに乗るとアラゴ大通りを通る。また、パリ天文台を通る子午線上には、ところどころ、写真のように南北を示すオブジェが埋められている。そこにはARAGO と記されている。