96.ニュートンの流率法
物理の授業をしていると、どうして微分や積分が物理に出てくるんだ、という文句が学生さんからよく出てくる。
でもね、力学の問題を解くために微分積分が生み出されたんだから仕方がない。
ライプニッツも同時期に微分積分学を考案していたものの、ニュートンは、力学の問題を扱うところから微分積分学を生み出した。力学は質点の運動の記述が大元にあるが、質点は運動しているので、もともと動的なものである。質点の運動の軌跡は、動点が辿る軌跡だ。平面曲線を考えると、平面はxとyの座標で表されるとすると、平面上の曲線は、ある関数 f(x,y)=0 で表される曲線に他ならない。例えば、半径 a の円は、f(x,y) =x 2 + y2 -a2 = 0 を満たす曲線だ。これを、点 (x,y) が“時間”とともに動いていった軌跡と考えるというわけだ。幾何学的に「原点からの距離 a が一定の点の集合」としてではなく、「動点が曲率一定(曲がり具合一定)で動いていった時の軌跡」を『円』と捉えるようなものだ。
動点が動いていく割合を、ニュートンは、「流率的速さ」あるいは単に「流率」と呼んでいた。そこで、ニュートン流の微分積分学は「流率法」と呼ばれる。
2次元平面で、“流量” x、 y の“流率”を、x'、y' と書くことにしよう。本当は x の上に黒丸・(ドット)を付けて書くのだが、フォントが無いので、代わりにダッシュを付けておこう。
こうして、各瞬間に描く無限に小さな線分の長さは速さに比例することから、O を“瞬間的時間”、x'、y' を x、y の流率(的速さ)として、ある瞬間に x、y であった長さは、次の瞬間には x + x'O、y + y'O になることが分かる。
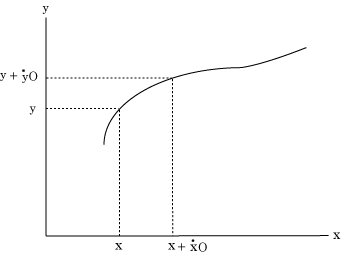
動点の曲線は f(x,y) = 0 で表されているので、
f(x,y) = 0
f(x+x'O, y+y'O) = 0
はともに曲線上にあるので、これらを連立させる。こうして、接線の傾きは、y 方向に動いた距離を、x 方向に動いた距離で割り算すれば得られるので、
y'O / x'O = y'/x'
として得られる。
具体的にやってみよう。
f(x,y) = x4 -ax2 -y
としてみる。f(x,y) = 0 の曲線とは、
y= x4 -ax2 ・・・(1)
のことだ。ここで、f(x+x'O, y+y'O) = 0でもあるので、代入して
f(x+x'O, y+y'O) = ( x+x'O)4 -a(x+x'O)2 -(y+y'O)
= 4x3 x'O-2axx'O-y'O+( O2 の項)+( O3 の項)+( O4 の項)
= 0 ・・・(2)
だ。ここで、(1)を使った。O は“瞬間的時間”であり小さいので、O2 、O3 、 O4 の項は小さいので無視しておき、(2)の両辺を O で割る。(2)の両辺を O で割ってから、残った O は小さいので無視すると言った方が良い。とりあえずやってみると、
4x3 x'-2axx'-y' = 0 、すなわち、y'/ x' = 4x3 -2ax
が得られる。この y' / x' が、点 (x,y) での曲線 f(x,y) = 0 の接線の傾きだ。これは今で言うところの、y を x で微分して得られる微係数を求めたことに他ならない。
では、微分の逆はどうだろうか。
1669 年にニュートンは、曲線の“下”の部分の面積、すなわち、曲線と x 軸に囲まれた面積を求める3つの規則を与えた。その内の「規則1」を見ておこう。規則1は
『もし、y = axm/n であれば、n / (m+n) × ax(m+n)/n が領域 ABC の面積に等しい』
というものだ。証明は「例から明らかである」と言って、ニュートンは6つの具体例を与えている。そのうちの一つが
「面積 S が、S = (2/3) × x3/2 となる曲線は?」
というものだ。ちょっと見ておこう。

図で、AB' の長さを x+O としておこう。AB の長さを x とするので、BB' の長さは Oだ。ただし、O は微小とする。今、長方形 BPQB' の面積が BCC'B' の面積と等しくなるように線分 PQ を引いたとする。BP の長さを v としよう。面積 S が S = (2/3) × x3/2 なので、両辺を 2 乗しておいて、
S2 = (4/9) x3 ・・・(2)
としておく。x が x から x+O に進んだ時の面積の増分は長方形 BPQB' の面積と等しいというのだから、BPQB' の面積は O×v より
(S + Ov )2 = (4/9) (x + O )3
が成り立っている。両辺展開しよう。
S2 +2SvO + v2O2 = (4/9) × (x3 +3x2O + 3xO2 +O3)
ここで、(2)から、S2 = (4/9) x3 であることを用いてから O で割ると
2Sv + v2O = (4/9) × (3x2 + 3xO +O2)
が得られる。ここでニュートンは
『もし BB' が無限に小さい、つまり O が零であると仮定すると、O がかかって
いる項は消え、かつ v は y に等しくなるので
2Sy = (4/9) 3x2 、すなわち y = x1/2
に還元される( S = (2/3) x3/2 を用いた)。』
として、問題を解いた。つまり、
『 y = x1/2 の曲線の下の面積( x 軸と囲む面積)は、S = (2/3) x3/2 である』
ここで、S = (2/3) x3/2 = 2 / (1+2) x(1+2)/2 であるので、ニュートンは
『S = n / (m+n) × ax(m+n)/n を取り上げ、面積 S を与える曲線は y = axm/n であ
ることを証明する予定である』
とした。この証明は簡単で、両辺 n 乗してから、上でやったことと同じことをすればできる。どうも、ニュートンは書き残していないようだが。
積分法の発見だ。1669 年、おそらく 1664 年から 1666 年の間に、ニュートンによる。
95.パスカルの三角形からニュートンへ
nを自然数として、( x + y )n の展開は比較的容易にできるが、逆の因数分解はなかなか難しい。
高校生になった息子が、
x4 + 4 y4 を因数分解せよ
という問題に出くわし、どうしたらよいかわからないようだった。
物理の研究を30年近くしている身にも、こんなに綺麗な数式を、なぜわざわざ因数分解するのか?という疑問を持つが、練習問題だから仕方がない。
結局息子は自分で解いたが、答えは
x4 + 4 y4 = ( x2 +2 x y + 2 y2 ) ( x2 -2 x y + 2 y2 )
左辺と右辺のどちらが美しいか?
でも、そんなこといったら、i = √(-1) という、2乗したらー1になる、つまり i 2
= -1 になる虚数単位を使えば
x4 + 4 y4 = ( x2 + i 2 y2 ) ( x2 - i 2 y2 )
= ( x + √2 i3/2 y ) ( x-√2 i 3/2 y ) ( x-√2 i 1/2 y ) ( x+√2 i 1/2 y )
= ( x + √2 ei(3/4)π y ) ( x-√2 ei(3/4)πy ) ( x-√2 ei(1/4)πy ) ( x+√2 ei(1/4)πy )
ともできるぞ?ここで、i 3/2 = ei(3/4)π =(-1 + i ) / √2、また、 i 3/2 = ei(1/4)π =(1 + i ) / √2
だ。
( 1 + x )n を展開した時の係数を、2項係数と呼ぶ。1665年、二項定理に現れる二項係数が、パスカルの三角形として簡単に表された。二項定理は
( 1 + x ) = 1 + x
( 1 + x )2 = 1 + 2 x + x2
( 1 + x )3 = 1 + 3 x + 3 x2 + x3
( 1 + x )4 = 1 + 4 x + 6 x2 +4 x3 + x4
・・・・
( 1 + x )n = nC0 + nC1 x + nC2 x2 + ・・・ + nCn xn
ただし nCr = n(n-1)×・・・×(n-r+1) / (1・2・3×・・・×r)
となる。ここで、xr の係数を並べると
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
・・・・・・・・・・・・
と三角形に並ぶが、中の数字は必ず、上斜め右と上斜め左の数の和になっている。例えば 5 段目の 6 は、右斜め上の 3 と左斜め上の 3 を足した数になっている。これをパスカルの三角形と言う。
少し並べ替えて、(1 + x )n の係数を縦に並べよう。一番上の段は、n の値。
|
n=0 |
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
1 |
3 |
6 |
10 |
|
|
|
|
1 |
4 |
10 |
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
1 |
そうすると、右へ右へ新たな数字を書き込むには、左斜め上と左の数字を足していけば良いことが見て取れる。たとえば、n = 5 の 3 段目の 10 は、左斜め上の 4 と左の 6 を足したものだ。空欄は 0 と思う。
ニュートンは、この表を、n が負の時に拡張した。一番上の段は、n の値。
|
-5 |
-4 |
-3 |
-2 |
-1 |
n=0 |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
← x0 |
|
-5 |
-4 |
-3 |
-2 |
-1 |
|
1 |
2 |
3 |
4 |
5 |
← x1 |
|
15 |
10 |
6 |
3 |
1 |
|
|
1 |
3 |
6 |
10 |
← x2 |
|
-35 |
-20 |
-10 |
-4 |
-1 |
|
|
|
1 |
4 |
10 |
← x3 |
|
70 |
35 |
15 |
5 |
1 |
|
|
|
|
1 |
5 |
← x4 |
|
-126 |
-56 |
-21 |
-6 |
-1 |
|
|
|
|
|
1 |
← x5 |
|
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
|
|
|
|
|
|
|
表は下へ、無限に続く。n が負の時の表の作り方は、右隣の数字から真上の数字を引くことで得られる。例えば、n = -3 の時の4段目、x3 の係数になる-10 は、右隣の-4 から真上の 6 を引く、つまり、-4-6 = -10 として得られる。こうして、n ≧ 0 のパスカルの三角形から、n が負の左側へ表を拡張していく。こうすると、例えば、n =-3をみていくと、確かに
( 1 + x )-3 = 1 - 3 x + 6 x2 - 10 x3 + 15 x4 -21 x5 +・・・
と、無限に続く二項展開が得られる。微分積分学を学んでテーラー展開を知っている人は、x = 0 の周りのテーラー展開をしてみるとよい。
1676 年には、ニュートンは、n が分数の場合の展開にも成功する。ただし、パスカルの三角形を直接拡張したものではないことを、1676 年の手紙で示している。( 1-x2 )n 、(n=0,1,2・・・) のグラフの下の面積を求める問題から、n = 1 / 2 の場合への補間を考えて得たそうだ。ニュートンが書いたように書くと(下付き棒線は本当は上に書いている、また分数は分数として書いている)
P +PQ |m/n
= P m/n + (m / n ) AQ + ( m-n ) / (2n) BQ + (m-2n) / (3n) CQ + (m-3n) / (4n) DQ +&c
ここで、P は第1項、Q は残りの項を P で割ったもの、A、B、C、D はすぐ前の項といったことだ。
具体例を見ておこう。( 1 + x ) 1/2 でやってみよう。1 + x の平方根だ。見比べると P = 1、Q = x、m = 1、n = 2 だ。A は前の項、Pm/n = 1 、B も前の項、(m/n)AQ =(1/2)×1×x、C も前の項、(m-n) / (2n) BQ = (1-2) / (2×2) ×(x/2) × xだ。こうして、
( 1 + x )1/2 = 1 + (1/2) x -(1/8) x2 + (1/16) x3 -(5/128)x4 +・・・
となることが確かめられる。これも、テーラー展開を知っていると確認できる。
94.゛機械学的”方法による求積
新学期が始まり、いつも2~3週間したら、黄金週間という名の連休が入る。今年、2019年は改元があり、10連休になった。
ずっと以前、大学に着任してまだ 5 年ほど、助手の頃に、共通教育という名の一般教育の授業で、「数学と物理学の進歩」だったか、「物理学の進歩と数学」だったかという名の授業を持つことになった。こういう科目は、ベテランの方が広い教養を活かしてお引き受け頂ければよいのだが、そういう発想がないのか、ようやらんのか、何故か私に回ってきた。
そこで、ネタ作りで、いろいろ調べた。もちろん、ニュートン力学と微積分や、一般相対論とリーマン幾何は話そうと思ったが、それだけだと話が広がらないので、沢山の本を読んだりして知識を集める。自分で講義ノートを作って板書しただけなので、すでに 20 年近くたってしまって講義ノートが散逸気味だ。そこで、残っている講義ノートをもとに備忘しておこう。
ニュートンやライプニッツの積分に行く前に、古来からの求積法を調べる。
そこで出くわしたものの一つが、アルキメデスの「方法」に書かれているという、放物弓型の面積の計算法だった。
図の太線で書かれた放物線に 2 点、A と C をとる。線分 AC に平行な放物線の接線を引き、接線が放物線に接する点を B とする。そうすると、放物線と線分 AC で囲まれた放物弓型の面積は、三角形 ABC の面積の 3 分の 4 倍に等しい。アルキメデスは、「てこの原理」を用いて示す。
まず、線分 AC の中点をとり、D とする。D と B を結ぶ直線を描く。D を通って放物線の焦点と頂点を結ぶ線分に平行な軸を引いたと考えても良い。その軸と放物線との交点が B だ。
次に、点 C で、放物線の接線を引き、線分 DB を延長した直線との交点を E とする。また、点 A から DB に平行に引いた直線が、点 C での接線と交わる点を F とする。三角形の辺 BC を延長して線分 AF と交わる点を K とする。さらに、CK を延長して、線分の長さが CK = KH となるように、点 H を取る。
さらに、直線 CK 上に勝手な点 N をとり、N を通り線分と DB と平行な直線を引く。この直線が CF と交わる点を M、CA と交わる点を O、放物線との交点を P とする。図の通り。

ここから、少し放物線の性質を使わせてもらう。
放物線の性質から、それぞれの線分の長さに関係がつけられる。まず、
EB = BD
これを使うと、三角形 CED と三角形 CMO が相似であることから、
MN = NO
が言える。
もう一度、放物線の性質を使わせてもらおう。
MO : OP = CA : AO
という比が、放物線であるということで得られる。これを使うと、三角形 CNO と三角形 CKA が相似であることから
MO : OP = CA : AO =CK : KN =HK : KN
が得られる。最初の等式は放物線の性質、2 番目は三角形の相似、3 番目は CK = HK と線分の長さをとって作図したことによる。第 1 式と第 4 式を取り出して書いておくと
MO : OP = HK : KN
になる。分数で書けば
MO / OP = HK / KN
だから、
MO × KN = OP × HK ・・・(1)
ということだ。
さて、ここからが機械学的だ。
まず、線分 CH を、点 Kを 釣り合いの中心とした“てこ”の棒と考える。また、OP と等しい長さの線分 TG を、その中心が H に来るように置く。図の通り。そうすると、(1)式は
MO × KN = TG × HK ・・・(2)
と書き直せる。ここで、てこ、またはシーソーの支点を K とし、MO と TG の線分が一様密度の棒と考えると、(2)式は、(重さ)×(てこの腕の長さ)が左右両辺で等しいという式になっている。左辺は、支点からの距離 KNに 、重さ MO を置いた式、右辺は支点からの距離 HK に重さ TG を置いたものと考えると、両者は釣り合っているという式だ。シーソーの釣り合いについては第 38 回参照。
N は勝手な点として CK 上に取ったので、この操作を点 N を CK 上を動かしていって、今までの操作を繰り返すと、放物弓型を構成する線分 OP を全部 1 点 H に集めたものと、線分 MO をその線分が置かれている各点での位置 N ごとにすべて集めたもの、すなわち三角形 FAC が釣り合うことになる。三角形 FAC を構成する線分は各点 Nごとに場所は異なっておかれているが、その重さを三角形の重心にすべて集めたものと同じになるので、三角形 FAC の面積に対応した重さを、三角形 FAC の重心においたと思えばよい。それが、放物弓型の面積に対応した重さと、支点 K で釣り合うというわけだ。三角形 FAC の重心は、線分 CK を 2 対 1 に内分する点、図では W であるので、
(放物弓型の重さ)× HK = (三角形FACの重さ)× KW ・・・(3)
となる。また
3 × KW = CK =HK ・・・(4)
である。W は CK を 2 対 1 に内分していることと、作図から CK = HK だったことを使った。さらに、最初の設定から
AC = 2 × AD
であったので、三角形の相似を睨んで
AK = 2 × DB
となり、結果、
AF = 2 × AK = 4 × DB
となるので、
(三角形FACの面積)=4 ×(三角形ABCの面積) ・・・(5)
となることが分かる。底辺 AC が共通で、高さ AF と DB が 4 倍違うからだ。
こうして、(3)の KW を(4)で HK にして、また三角形 FAC を(5)を使って三角形 ABC に置き換えると
(放物弓型の重さ)× HK = (三角形FACの重さ)× KW
= 4 ×(三角形ABCの重さ)× HK / 3
なので、重さと面積が比例していることから
(放物弓型の面積)= ( 4 / 3 ) ×(三角形ABCの面積)
が得られる。
確かに、放物線と線分 AC で囲まれた放物弓型の面積は、三角形 ABC の面積の 3 分の 4 陪に等しいことが言えた。
面積を求める際に、物理のてこの原理を使うとは、さすがアルキメデス。「支点とてこを与えられたら地球を動かして見せよう」と言っただけのことはある。
93.授時
第69回で、宇宙観の進展について備忘した。どうしても西洋中心の宇宙観になってしまうが、中国ももちろん古くから進んでいた。
初期中国では、宇宙の空間的構造としては 3 つの説が唱えられていた。1 つ目は天地は平面的とした蓋天(がいてん)説。天と地は平行であり、離れた2点から太陽の高度を図り、天の高さは 80,000 中国里、多分およそ 5,700 kmと見積もっていた。後に天はお椀をかぶせた形に変更している。2 つ目は渾天(こんてん)説で、天界は鶏卵の殻の様に天球から成っていて、大地は鶏卵の黄身にあたるような宇宙の形だと考えた。3 つ目が宣夜(せんや)説で、宇宙は無限の虚空であり、天体は自由な空間に浮かんでいるとした。
西洋の天動説に近いのは 2 番目の渾天説だ。
キリスト紀元 78 年に生まれ、139 年に亡くなる中国、後漢時代の大科学者、宮廷天文官であった張衡(ちょうこう)は、渾天説に立っていたようだ。しかも、地球は宇宙に浮いた球体で、九大陸を持つと考えていた。彼は、それまでにあった天体観測用の天球儀を改良したうえで、天体観測を行って星々を記録していったようだ。それに飽き足らず、水力で動く天球儀を作り、締め切った部屋の中で水力により天球儀を回転させ、動く天球儀にあわせて、これこれの位置に今、何々の星が南中するはずだとか昇ってくるはずだとか指令を出し、部屋の外で観測している者が本当に、水力で動く天球儀の予言通りに星々が現れたりするか確認したところ、張衡の言う通りだったそうだ。
張衡はまた、地動儀、現在言うところの地震計を発明している。青銅でできた甕の周囲に 8 匹(8頭?)の龍がついていて、それぞれの口に青銅の球を加えており、地震が来て揺れを感じると、龍の口から球が落ち、下で待ち構えている青銅製の蛙の口に入るというようになっている。地震で落ちる球は 1 つで、これにより震源の方向も分かるらしい優れものだ。後漢書に、「一つの球が落ちたが感じる揺れは無かった。ところが、数日後に都にやってきた使者が、都から(今の距離で) 640 km 離れた場所で地震があったと伝えた」とあり、実際に機能していたようだ。

国立科学博物館、張衡「地動儀」の復元模型
張衡はまた、円周率πの値の計算も行っている。彼は、およそ3.16と与えた。後に、紀元 400 年代末、500 年より少し前に、祖沖之(そちゅうし)が、円に内接する正24,576 角形の辺の長さを計算し、それが円周の長さに近いものとして、円周率は3.1415926 と 3.1415927 の間だと結論づけている。西洋文明がこの結果を得るのは、紀元 1,600 年頃なので、この時点で 1,100 年くらい先んじていた。
さて、張衡は文人でもあり、例えば 6 世紀に編纂された「文選」に彼の「帰田賦」が収められている。後漢の安帝に召されるも、安帝は宦官の専横を許して政治が乱れ、次に宦官に擁立された順帝のときに職を辞して故郷に帰るときのことを謳った賦が帰田賦だ。というわけで、「都住まいも永くなるが、世の中を良くする助けもできず、川に臨んで魚を取ることを願い、河が清く澄む時世を未だ待つ」といった感じで始まる。政(まつりごと)は乱れている。
その文選であるが、清少納言の枕草子にも「書は、文集。文選、新賦。史記、五帝本紀。願文。表。博士の申文。」とあり、「書(ふみ)は白氏文集。文選、特に新賦が良い。(以下略)」と言っているので、公家の常識だったのだろう。遡って飛鳥から奈良時代の知識人である大伴旅人も、6 世紀に編まれた文選は当然知っていただろう。万葉集の梅花歌三十二首の序を書いた大伴旅人は大宰府に居てそれを編んだそうだが、何故太宰府かと言うと、当時権力を握っていた藤原四兄弟、武智麻呂(むちまろ)、房前(ふささき)、宇合(うまかい)、麻呂(まろ)に左遷されていたという説があるようだ。梅花歌が詠まれる前に、藤原四兄弟が無実の罪で長屋王を追い詰め自殺させるという長屋王の変が起きている。まつりごとは乱れていた。
もう、語り尽くされていることではあるが、備忘として記しておこう。
大伴旅人は、梅花歌序で「于時 初春令月 気淑風等和」と記す。「初春の麗しい月であり、気候も良く風は穏やかだ」と。これは、張衡の帰田賦の「於是仲春令月 時和気清」(これにおいて、春半ばの麗しい月、時節は和やかで、大気は澄んでいる)を踏まえているのだろう。梅花歌自体は花を愛でるような歌だが、大伴旅人は序を書くことで読者に張衡の帰田賦を想起させ、張衡が都を離れて故郷に帰らざるを得なかったと同じく、乱れた政治の世であることを意識させる装置を仕込んでおいたようだ(「「令和」から浮かび上がる大伴旅人のメッセージ」品田悦一(東京大学総合文化研究科教授))。さすが、万葉集の研究家。指摘は鋭い。
古代中国では、天子(皇帝)は天帝の天命を受けて「宇宙」、宇は空間、宙は時間のことであるが、これらを支配するものとされた。時間を支配する具体として、人民に暦を授けていた。暦作成のために天文官を置き、詳細な天体観測を行っていた面はある。これを観象授時と呼ぶ。支配者や王朝が変わった時には、新たに天命を受けたとして改暦を行う。天の命が革(あらた)まったときには王朝を倒す革命が起きるというわけだ。
張衡が亡くなってから 50 年後に、後漢の少帝が殺され、統治機能を失う。さらに 30年後に、後漢は滅び、魏、呉、蜀が並ぶ三国時代に入る。
92.漱石から採る物理の問題
子供が、入試勉強で、国語や英語の長文問題では問題を解く時間が無くなるとぼやいていた。そういう時は、問われている問題を先に読んでから、問題文である長文に目を通したら、どこに答えが潜んでいるかわかりやすい、と助言しておく。長文読んでから問題を読むと、問われたことをまた長文の中から探さないといけなくなるので二度手間だ。
物理でも、長文読解できないかと考えてみたが、アイデアが無い。そこで、ちょっとした遊びで、夏目漱石を引用して問題にあたらせてみた。
寺田寅彦が「吾輩は猫である」の寒月君のモデルになっていることは有名な話だ。寺田寅彦は、現在の高知県立追手前高校、旧制の高知県尋常中学校を卒業後、熊本の旧制第五高等学校に進学した。そこの英語の先生が漱石であり、その後、親交が続く。漱石の「三四郎」では、三四郎の同郷の理科大学の教師の野々宮さんのモデルが寺田寅彦だ。
そこで、「三四郎」を引用し、こんな問題を作る。数式をいじらせるのではなく、概念を述べさせる目的だ。
『(「三四郎」から引用)
「物理学者でも、ガリレオが寺院の釣りランプの一振動の時間が、振動の大小にかかわらず同じであることに気がついたり、ニュートンが林檎(りんご)が引力で落ちるのを発見(1)したりするのは、はじめから自然派ですね」
「そういう自然派なら、文学のほうでも結構でしょう。原口さん、絵のほうでも自然派がありますか」と野々宮さんが聞いた。
問1. 下線部(1)に関して、ニュートンが発見した引力の法則は、「万有引力の法則」と呼ばれている。万有引力の法則に関して、その数学的表現を書き,法則の物理的な内容をあわせて記しなさい。また、万有引力の法則により理解できる自然界の事実について述べなさい。』
『(「三四郎」から引用)
「野々宮さん光線の圧力の試験はもう済みましたか」
「いや、まだなかなかだ」
「ずいぶん手数がかかるもんだね。我々の職業も根気仕事だが、君のほうはもっと激しいようだ」
「絵はインスピレーションですぐかけるからいいが、物理の実験はそううまくはいかない」
(中略)
「我々はそういう方面へかけると、全然無学なんですが、はじめはどうして気がついたものでしょうな」
「理論上はマクスウェル(2)以来予想されていたのですが、それをレベデフという人がはじめて実験で証明したのです。近ごろあの彗星の尾が、太陽の方へ引きつけられべきはずであるのに、出るたびにいつでも反対の方角になびくのは光の圧力で吹き飛ばされるんじゃなかろうかと思いついた人もあるくらいです」
批評家はだいぶ感心したらしい。
問2.
下線部(2)に関して、電磁気学に関する真空中のマクスウェル方程式を書きなさい。また、マクスウェル方程式は、ベクトルの方程式として4組現れるが、それぞれについて、物理的な意味合いを述べなさい。』
みたいな感じ。
問題を解いた学生諸君は、夏目漱石の小説に興味を抱いたかしらン?
91.CP対称性の破れ
前回、鏡のこちらと向こう側では自然法則は同じでなくなり、こちらの世界で起きる事象が、あちらの世界では禁止されることがあることを、コバルト 60 の放射性崩壊を例にして、見た。最後に指摘しておいたように、さらに、粒子・反粒子を入れ替えると、鏡のこちらでも向こうでも自然法則が同じになることも見た。
鏡に映す操作は、空間座標をすべて反転させる操作と同じになるので、空間反転と呼ぼう。特に名前がついていて、パリティ変換という。頭文字をとって、P 変換と呼ぶことにする。粒子・反粒子を交換する操作は荷電共役変換と呼び、C 変換と呼ぶ。荷電が“チャージ”なので、頭文字の C をとって C 変換。P 変換して、続いて C 変換する操作を CP 変換といい、前回みたように自然法則が CP 変換で不変になったので、“C P対称性がある”という言い方をする。
ここから少し専門的になってしまうが、後のために少し書いておこう。
ミクロの世界では“量子力学的状態”というもので、状況が指定される。ある状態を
| Ψ(x,y,z) >
としよう。空間を反転させると
| Ψ(-x,-y,-z) >
という状態になるが、“量子力学的”に事象が起きる“確率”は状態 |Ψ> の“絶対値の 2 乗”に比例する、と言うのがミクロの世界の“掟”なので、空間反転すると
| Ψ(x,y,z) > (空間反転:P変換)→ α | Ψ(-x,-y,-z) >
と、絶対値 1 の定数 α がつくことが許される。α は複素数で良い。もう一度空間反転して見よう。
| Ψ(-x,-y,-z) > (空間反転:P変換)→ α| Ψ(x,y,z) >
となるはずだから、2 回空間反転して
| Ψ(x,y,z) >(空間反転:P変換)→ α | Ψ(-x,-y,-z) >
(空間反転:P変換)→ α×α | Ψ(x,y,z) >
となる。2 回空間反転すると元に戻るはずだ。2 回鏡に映すとこちらの世界と同じになるんだから。そうすると最後の
α×α | Ψ(x,y,z) >
は、もともとの
| Ψ(x,y,z) >
と同じでないといけない。というわけで
α×α | Ψ(x,y,z) > = | Ψ(x,y,z) >
だから、
α×α = 1 、つまり α = ±1
であることがわかる。こうして、世界の状態は 2 つに分けられた。
| Ψ(x,y,z) > (空間反転:P変換)→ | Ψ(-x,-y,-z) > (α=1)
| Ψ(x,y,z) > (空間反転:P変換)→ -| Ψ(-x,-y,-z) > (α=-1)
ここで出てきた α = 1 または-1、を、その状態が持つ“パリティ”と呼ぶ。
さて。
K 中間子という素粒子がある。その中で、電荷が 0 の K 中間子を K0 、その反粒子をK0 と書くことにしよう(反粒子は、本当は上に棒線を付けるのだが、フォントがないので下に付けた)。K 中間子の状態は、空間反転で、符号を変える側、パリティマイナスである。いちいち、“(空間反転)→”と書くのも、あんまりなので、空間反転、パリティ変換を P であらわし、
P| K0 > = -| K0 >
と書く。続いて、粒子・反粒子を変える C 変換を施すと、
C P| K0 > = -| K0 > ・・・(1)
と、マイナスが付いたまま、反粒子 K0 の状態 | K0 > になる。同じように
C P | K0 > = -| K0 > ・・・(2)
だ。“量子力学的状態”は粒子の“波動性”から、重ね合わさる。普通の波が二つ、右と左からやって来たら、重なり合うようなものだ。そこで、
| KS > = (| K0 > -| K0 > ) / √2
| KL > = (| K0 > +| K0 > ) / √2
と、元の K 中間子の状態を重ね合わせた状態を考えると、(1)、(2)式から
CP | KS > = | KS >
CP | KL > = -| KL>
のように、CP 変換で元の状態に戻り、かつ決まった符号を持つことが分かる。| KS > 状態は CP=プラス 1、| KL> 状態は CP=マイナス 1だ。
さて、K 中間子はパイ中間子に崩壊する。電荷が 0 のパイ中間子は、空間反転するとやっぱりマイナスが付いて元に戻る。
P | π0 > = -| π0 >
電荷が 0 のパイ中間子の反粒子は、自分自身になっている。というわけで
CP |π0 > = -| π0 >
K 中間子は、2個、または 3 個のパイ中間子に崩壊する。そのとき、自然界がCP 変換で不変であれば、崩壊前の CP の値と、崩壊後の CP の値は保存されて同じはずだ。π0 中間子の CP はマイナス 1なので、2個に崩壊するときには(-1)×(-1)= + 1、3個に崩壊するときは(-1)×(-1)×(-1)= -1 という CP の値を持つ。こうして、CP が +1 の KS 状態は2個のパイ中間子に、CP が-1 の KL 状態は3個のパイ中間子に崩壊することになる。
KS 状態は KL 状態より短い時間で2個のパイ中間子に崩壊する。KS 状態は KL 状態より寿命が短いというわけだ。ということで、十分時間を置いておけば、KS 状態は2個のパイ中間子に崩壊してしまって、もはや残っておらず、長時間後は KL ばかりになので、3個のパイ中間子にのみ崩壊する。
ところが。
KL 状態なのに、2個のパイ中間子に崩壊する事象が見つかってしまう。1964 年のことだ。実験で発見したクローニンとフィッチは 1980 年にノーベル賞を貰う。この発見が何を意味するかというと、自然は CP 変換の下で不変ではない、CP 対称性は“破れる”ということだ。
なかなか手ごわい。
どうして CP 対称性が破れるか。それを明らかにしたのが、小林誠さんと益川俊英さんの、小林・益川理論で、クォークが 6 種類あれば説明できるというものだ。1973 年のことだ。小林・益川両氏も 2008 年になってからノーベル賞を貰う。
さてさて。
理論的に確実なのは、さらに時間反転させてやると、必ず自然法則は不変になる、というものだ。時間反転を T 変換ということにすると、これは CPT 定理と言って、空間反転、荷電共役変換、時間反転を続けて行うと、必ず自然法則は不変になるという強力な定理。
ということは、CP 対称性が破れているということは、必然的に T 変換、つまり時間反転対称性も破れているということだ。だって、T 変換だけ破れてなかったら、CPT と続けて変換したとき、CP の破れのみ残って、元に戻ってくれなくなるから。
というわけで、K 中間子の CP 対称性の破れから、時間反転対称性も破れていなければならないということが言える。
某大学で学生をやっていた時代、一人ずつ執筆する 4 回生の卒業論文というものは無く、8人のグループで1年間かけて一つの課題に取り組む“課題研究”という方式がとられていた。理論も実験も行って、最後に8人で纏めるというもの。私は、“時間反転対称性の破れの検証”みたいな、原子核反応を扱う課題研究を選んだ。4回生の学生実験なので、まぁ、画期的な結果は出ないだろうが、総合的にいろいろ学ぶということが大切だった。時間反転の理論を学び、実験では回路や真空技術や検出器作成や加速器などについて学んで、実際に実験を行った。自分たちで検出器を作ったり、原子核をぶつけるターゲットを作ったり。検出器は SWPC(Single Wire Proportional Chamber、単芯比例計数管)を作り、実際に作用することを確かめた。多芯(Multi Wire)にしたかったんだけれど。でも、まだ、実験の才能はかすかに残っていた。実験としては、炭素12、12C 原子核に重水素の原子核、d を衝突させて、炭素 13、13C 原子核と陽子、p に変える原子核反応実験を行う。時間反転した事象は、炭素 13、13C 原子核に陽子をぶつけ、炭素 12、12C 原子核と重水素の原子核、d を生成するということになる。
12C + d ⇔ 13C + p
こうして、両側からの原子核反応の割合を比較して、時間反転不変性が成り立っているか、破れているか、破れているならどれくらいかを調べようという実験であった。炭素12はありふれた元素なので、ターゲットは食品ラップを使った。サランラップはポリエチレン(炭素と水素がつながったもの)以外にいろいろ添加されていたので、原子核反応ではノイズになる。クレラップは、ポリエチレンのみで作られていたので、それを採用した。炭素 13 は自然界にそうないので実験担当の教員にねだって買ってもらった。実験の結論は、時間反転対称性は、まぁ、破れていないし、破れているとしても、これこれ以下というものだったと思う。
何より思い出に残っているのは、本実験で、タンデム・ヴァンデグラフ加速器という加速器を動かし、実際に原子核反応を起こさせたことだ。実験データを取るために検出器の設定、ターゲットの設置、複雑な回路を組むといったことを行う。回路を組んでいるときに、あぁ、自分はやっぱり実験屋は無理だと悟った。現在はT帝国大学教授になってしまった Y 君が、複雑な回路をちゃっちゃと繋いで、モジュールを組んでいった。今でも立派な素粒子物理学実験屋さんだ。加速器のマシンタイムもそう呉れないので、一旦動かしたらできるだけデータを取りたかった。8 人のグループだが、一人欠け、二人下宿に帰り・・・で、1日徹夜で実験したが、さらに夜が明けた翌日も 1 日実験し、最後まで加速器棟で加速器を動かしてデータを取っていたのは、Y 君と私だけになった。順方向と逆方向の原子核反応のデータを検出器の角度を変えたりしながら兎に角溜めた。1晩寝ていない上に 2 晩目の深夜。さぁ、私たちの学生実験グループに割り当てられている実験の時間も終わるので、終了しなければ、という時間になった。朝、明け渡すので、そろそろ終わろうと Y 君と相談したのは、おそらく徹夜 2 日目に入った午前3時ころだったか。加速器棟には、最初に加速器から加速された原子核ビームを引き出すときの調整とか、専門的な技能を持った技官の方がいたが、そんな深夜なので当然帰宅されている。そこで、実験担当の教員のご自宅に電話した。そんな深夜なのに。で、実験終わりましたが、加速器立ち上がったままなんですが、技官の方もおられないのでどうしましょう、と相談すると、そんな深夜なので、お前ら2人で加速器止めとけ、というお達し。加速器運転のマニュアルがどこそこにあるから、その手順通りにやったら良い、との仰せ。加速器止めるなんて…。どっかで手順間違えて、加速器壊したら何億円なんだ?という当然の疑問には、加速器壊れても構わないから2人でやってみなさい、とのこと。
教育だなぁ。指導教員、度胸あるなぁ。
まぁ、加速器の更新が近かったからなのかもしれないが、でもまだ、加速器を動かして実験する予定はあったはずだ。
で、Y 君とマニュアルを探して、加速器本体に入った。普通だったら学生は絶対入れてくれない聖域だ。放射線濃度も高いし。なんやらわんわん音が鳴っている中、マニュアルに従って、加速器を止めていく。結構な手順があった。途中、ゴムの靴がおいてあって、それに履き替えて作業することになっていた。高電圧を止めないといけない場所で、感電しても触った手から体を通って足を抜けて地球に電流が流れていって死んでしまわないための防護だった。ひぇ~っ。
しかし、そこは将来優れた実験物理屋になる Y 君がいたので心強い。間違えずに、順々に加速器の停止に向けて作業を行い、無事にシャットダウンできた。
放射線量計とか返して、加速器棟の電気消して、鍵かけて、バイクのY君とバイバイ。
その後は下宿で爆睡だった。
90.鏡の向こうとこちらの物理
前回、89 回では、鏡の向こう側が何故、右と左が反対に見えるのか、あるいはそう感じるのかについて考察した。人とかだと、あからさまに左右が違う。例えば顔のほくろの位置とか、心臓の位置とか。でも、基本の基本の自然法則までたどれば、自然は鏡のこちらの世界と向こうの世界を区別しているのだろうか? 言うなれば、右と左は区別がつくのか?
素粒子の世界まで行くと、起きている現象を見て、鏡のこちらで起きている現象なのか、鏡の向こうで起きている現象なのか、一見しただけではわからないだろう。素粒子が動いている現象を鏡に映しても、自然な運動に見える。右方向に動こうが、左方向に動こうが、どこにも不思議さを感じさせない自然な現象だ。だから、物理学者も、自然法則は右と左を区別しない、すなわち鏡のこちらの世界で起きる現象は、鏡に映しても同じように生じると考えていた。前回やったように、鏡の面に垂直方向におかれた矢印の向きは鏡に映すと反転するが、鏡の面に平行な平面上に置かれた矢印は反転しない。x-y-z 座標を考えると、どれか一つの軸が反転して、残りの 2 軸は反転しないというわけだ。しかし、すべての座標軸を反転させてからうまく回転させてやると、1 本だけ反転させた座標軸と重なるので、鏡に映すことを“空間反転させる”ということにしよう。そうすると、「自然法則は空間反転しても不変である」と言えそうだ。
私たちのよく知る電磁気現象では、右と左を区別するような現象は見られない。鏡の向こう側の世界も自然な世界だということだ。「空間反転対称」な世界だ。
ところが。
自然界には私たちのよく知っている電磁気力や万有引力の他に、原子核の放射性崩壊を引き起こす“弱い力(弱い相互作用)”と呼ばれる力が存在している。この力は原子核程度の大きさの中の距離でしか働かず、しかも力が“弱い”ので、私たちの日常には現れてこない。しかし、この力は、ある種の原子核を別の原子核に自然に壊変する際や、素粒子が他の素粒子たちに崩壊する際に働く。1950 年代初め頃に弱い相互作用で崩壊する素粒子に不思議な現象が見られた。質量などは全く同じなのに、一つの素粒子は 2 つの π 中間子に、もう一つの素粒子は 3 つの π 中間子に崩壊する。その現象をよく吟味した T.D.リーと C.N.ヤンは、実は弱い相互作用では鏡のこちら側で起きる自然現象は、鏡の向こうでは禁じられている、つまり「自然は空間反転不変ではない」のでは、という論文を書く。1956 年のことで、検証実験をあわせて提案する。1957 年に提案を受けたC.S.ウーは実験を行い、本当に鏡のこちらと向こうでは異なることを示す。
コバルト 60(60CO)という原子核がニッケル 60(60Ni)という原子核へ、電子(e-)と反ニュートリノ(νe)を放出して崩壊する現象を考える。素粒子や原子核には固有の角運動量-スピンと呼ばれる-を持っている。自転と考えてはいけないのだが、話を単純化するために、“自転”の(スピン)角運動量としてみる。回転方向に右手の 4 本指を添わせて包み込んだ時、親指の立つ方向が、スピンの向きだ。図の左側、崩壊前にはコバルト原子核は(スピン)角運動量 6 を持つ。上向きなので、+6。この 60CO が崩壊し、60Ni と電子、反ニュートリノ(ニュートリノの反粒子なので、上に棒線(バー)を付けて表わしている)になる。図の右側。60Ni の(スピン)角運動量は +5、電子も反ニュートリノも +1/2、全部合わせて +6。崩壊前と崩壊後で(スピン)角運動量の値は変わっていない。角運動量の保存則が成り立っているからだ。電子は、図のように下側に、反ニュートリノは上側に放出される。電子は、その運動方向とスピンの向きに制限はないが、反ニュートリノのスピンの向きは、その運動方向と同じものしかない。運動方向に右手の親指を立てて 4 本の指を包むと丁度ニュートリノの“自転角運動量”が再現されるので、反ニュートリノは『右巻き』だと言われる。こうして角運動量の保存法則が成り立つためには、反ニュートリノの(スピン)角運動量も電子の(スピン)角運動量も図のように上を向いていないといけない。しかし、反ニュートリノは、その(スピン)角運動量が反ニュートリノの運動方向と同じ向きのものしか存在しないので、上向き(スピン)角運動量を与えるためには、上方向に進むしかない。こうして、実際の実験でも、反ニュートリノはもともとの 60CO の(スピン)角運動量の方向にのみ放出され、電子は(運動量保存法則も満たさないといけないので)反対方向に放出される。放出方向に非対称性があるということだ。これは実験事実。

さて、この現象を鏡に映してみよう。図が 2 つあるが、下左図は崩壊前、下右図が崩壊後で、ともに“鏡”と書いた平面の左側が現実世界、右側が鏡の向こうの世界だ。

角運動量を“自転”と考えると、鏡に映すと“自転”の回転の向きが反対になるので、右手の 4 本指で回転方向に沿って包んだ時に親指が立つ方向 -(スピン)角運動量の方向-は、鏡の向こうではこちらと反対になる。だから、鏡の向こうでは 60CO の(スピン)角運動量は大きさが 6 で向きは下、-6 だ。崩壊後の図を見てみよう。60CO も 60Ni も静止しているが、崩壊後に出てきた電子(e-)と反ニュートリノ(νe)は運動している。しかし、鏡に映しても、運動方向は変わらない。鏡に平行な平面上の矢印だから、鏡に映しても反転しない。変わるのは、(スピン)角運動量の方向だ。電子の“自転”もニュートリノの“自転”も鏡に映すと反対向きになるので、(スピン)角運動量の方向は、鏡に映すと反対になる。そうすると、鏡の向こうの世界では、電子の(スピン)角運動量、反ニュートリノの(スピン)角運動量ともに、“下”を向くはずだ。こうして、右図の鏡の向こう側-右側-の状況になる。
しかし。
鏡に映しても同じ現象が起きるなら、鏡の向こうの反ニュートリノの(スピン)角運動量の方向は、進行方向と反対向き、つまり『左巻き』でないといけない。しかし、現実世界には『左巻き』の反ニュートリノは存在しない。それは鏡の向こうでも同じはずだ。
いや、正確に言うと、『左巻き』反ニュートリノは存在するのだが、『左巻き』の反ニュートリノは「弱い相互作用」が働かないのだ。つまり、「弱い力」が引き起こす放射性崩壊には関与しない。
こうして、「弱い相互作用(力)」が関与する場合には、鏡のこちらで見られる現象が、鏡の向こうでは存在しない。鏡に映した世界は成り立たないというわけだ。だって、そんな反ニュートリノは存在しないのだから。

なんとなく、鏡に映しても自然法則は同じであると思っていたのが、そうではないとわかるとビックリする。リーとヤンは論文を書いた 1956 年の翌年、1957 年に、この業績でノーベル物理学賞を貰う。T.D.リー 31 歳、C.N.ヤン 35 歳のことだ。「空間反転対称性の破れ」を実験的に示したウーさんは、ノーベル賞を貰えなかった。
もう一歩先へ。
鏡に映した後、粒子と反粒子を入れ替える。60COは、反陽子と反中性子からなる反コバルト 60 に変換される。放射性崩壊で、反ニッケル 60 と、陽電子と呼ばれる反電子と、反ニュートリノの“反”粒子であるニュートリノに崩壊する。(スピン)角運動量や放出される粒子の運動方向は、粒子と反粒子を入れ替えてもかまわない。そうすると、2つ前の図の崩壊後の粒子をすべて反粒子に置き換えると、今度は左巻きのニュートリノが図の上方に放出される図になる。左巻きのニュートリノは存在するので、反コバルト 60 の放射性崩壊は、鏡に映して(P変換)から粒子・反粒子を入れ替える(C変換)操作をすると、現実世界と同じになる。こうして、鏡に映したら自然法則は同じでなかったが、さらに粒子・反粒子を入れ替えると自然法則は同じまま成り立つことが分かった。これを CP 不変性という。
でも、まぁ、今回の本題の、粒子・反粒子は入れ替えずに、鏡に映しただけでは自然法則は不変でない場合があることはわかった。