99.黄金比
息子も高校生となり、数学の先生から授業以外の数学の話を聴く機会が増えた様だ。先生が黄金比の話をしたようで、詳しくなっていた。教科書以外の知識が学問への導入になることは多い。
そういえば、自分自身も、正五角形の黄金分割の話を何かで読み、興味を持っていたことを思い出す。

図のように正五角形を書こう。三角形ABC と ACD と ADE の 3 つから 5 角形が作られるので、正五角形の内角の和は、180 度 × 3 = 540 度となり、正五角形の内角一つは540 ÷ 5=108 度だとわかる。三角形ABE を考えると、これは二等辺三角形で、しかも角BAE が 108 度なので、角ABE と角AEB はともに 36 度になる。正五角形の 2 頂点を結ぶ線分は BE だけでなく、AC も同じだ。だから、同じく、角BAC(=角BAF )も、角ABE(=角ABF )と同じく 36 度だから、三角形FAB は二等辺辺三角形になる。底角FBA と FAB が等しいから。こうして、三角形ABE と三角形FAB は相似だ。だから、それぞれの三角形の辺の長さの比として
AB : BE = BF:AB つまり AB / BE = BF / AB
だから、
(AB)2 = BE × BF ・・・(1)
となる。
また、角EAF は、角EAF =角BAE -角BAF = 108 度-36 度 = 72 度となり、角AEF = 3 6度だったので、三角形EAF を考えると、角EFA=180度 - 角AEF - 角EAF =180度-36度-72度=72度なので、三角形EAF も二等辺三角形であることがわかる。こうして辺の長さは AE = EF である。
今、正五角形の辺の長さを 1 としておくと、
AB = AE = EF = 1
である。さらに、対角線の長さ BE に対して、BE = x とすると、EF =1よ り、BF=x-1 になる。こうして(1)式から
12 =x ( x-1)
という式が得られる。整理すると、
x2 - x -1 = 0 ・・・(2)
となる。こうして、この2次方程式を解くと、
x = ( 1 + √5 ) / 2 (>0)
が得られる。こうして、
BF :FE = x-1 : 1
= x2 - x : x
= 1 : x
が得られる。1 行目から 2 行目は、比の値にそれぞれ x を掛け、2 行目から 3 行目へは(2)式から x2-x = 1 であることを使った。こうして正五角形の対角線は、他の対角線で、1:x に分割されることが分かった。この分割を、黄金分割と呼び、比
x = ( 1 + √5 ) / 2 =φ
を黄金比と呼ぶ。あらたに、φ という文字で定義した。φ はもちろん(2)式の正の解。√5 なんて無理数が入っているので、大体の数値を見ておくと
φ = 1.618033989・・・
さて、黄金比 φ が得られたが、下の図のように、辺の長さが φ と φ2 になる長方形ABCDを考えておこう。φ で割っておくと、変の長さの比は、
1 : φ
だ。φ は(2)式を満たすので
φ+1= φ2 ・・・(3)
だから、一辺の長さ φ の正方形AEFD をとると、長方形EBCF が残る。この長方形の辺の長さは図のように 1 と φ だ。1 になるのは(3)式から、φ2-φ=1 だから。
こうして、辺の長さが 1:φ(=φ:φ2 ) の長方形から正方形を取り除くと、また辺の長さが 1:φ の長方形が得られる。何度やっても同じだ。

そこで、下図のように次々正方形を取っていって、ついでに各正方形に 4 分の 1 の円を内接させていくと、アンモナイトの貝殻を横から見た様な図になる。生物は、進化の過程で、黄金比を知ることになったのだろうか。


さてさて、幾何学から離れてみよう。
黄金比 φ は、次のような式で表される(フォントが無いので見にくい・・・)。
φ = √(1+√(1+√(1+√(1+・・・
つまり、ルート(1+ルート(1+ルート(1+・・・)と、ルートの中に1+√・・・が繰り返し現れる。証明は簡単で、右辺を x とおくと、最初のルート(1+・・・)を考えると、・・・の部分はまたxそのものだから、
x = √(1 + x )
に他ならない。2 乗すると
x2 = 1 + x
となり、これは黄金比を求めた際の(2)式だから、解いて正の解を取ったら φ になる。
また、黄金比は連分数でも表される(フォントが無いのでちょっと書けないなぁ)。

右辺の1+の次の分数の分母も、1+となっていて、これは φ そのもの。そこで、φ の代わりにまた x と書くと、
x = 1 + 1 / x
となるので、x を掛けると
x2 = x + 1
となって、やっぱり(2)式だ。だから、解は黄金比 φ に一致する。
さてさてさて、黄金比 φ の逆数を見ておこう。
1 /φ = 2 / (1 + √5 ) = 2×( 1-√5)/ ( ( 1 + √5)×( 1-√5 ) )
= -( 1 -√5 ) / 2
= ( 1 + √5 ) / 2 - 1
= φ- 1
となる。計算するまでもなく(3)式を両辺 φ で割ると得られる式だ。何が言いたかったかと言うと、黄金比の逆数 1 /φ は黄金比の小数点以下の部分、0. 618033989・・・を表しているということ。φ から、整数部分の 1 を引いているから。
フィボナッチ数との関係も見ておこう。
一つがいの兎がいた。1 年目は成長するだけで何も起きないので、1 年後、つまり 2年目も兎は一つがいだ。2 年目中に一つがいの兎を産む。こうして、3 年目(の初め)には 2 つがいの兎がいる。4 年目にも一つがいの兎を産むが、昨年生まれたつがいの兎はまだ子を産まないので、4 年目には全部で 3 つがいの兎だ。5 年目には最初に生まれた兎が成長して一つがいの兎を産む。もとからいた一つがいの兎も一つがいの兎を産むので、5 年目には全部で 5 つがいだ。こうして数列を書いていくと、
1、1、2、3、5、8、13、21、34、55、89、・・・ ・・・(4)
となる。この数列は
Fn+2 = Fn+1 + Fn , (n=1, 2, 3, ・・・) ・・・(5)
と表される。これを提案者の名前を取って、フィボナッチ数、フィボナッチ数列と呼ぶ。たとえば、フィボナッチ数の 5 番目は(4)の 5 番目、5 だ。6 番目は 8 だから、(5)式に当てはめ、
F7 = F6 + F5 = 8 + 5 = 13
と、正しく(4)の並びの 7 番目の数が出ている。
このフィボナッチ数列で、一つ前の数字との比を取ってみる。例えば、
F4 / F3= 3 / 2 = 1.5
F5 / F4 = 5 / 3 = 1.6666666666・・・
F6 / F5 = 8 / 5 = 1.6
F7 / F6 = 13 / 8 = 1.625
F8 / F7 = 21 / 13 = 1.615384615・・・
F9 / F8 = 34 / 21 = 1.619047619・・・
F10 / F9 = 55 / 34 = 1.617647059・・・
F11 / F10= 89 / 55 = 1.611818181・・・
と、なんとなく、黄金比、1.618033989・・・に近づいてくるようだ。調子にのって、もっと計算すると
F20 / F19 = 6765 / 4181 = 1.618033963・・・
うん、近い。もうちょっと。
F50 / F49 = 12586269025 / 7778742049 = 1.618033989・・・
いい感じだ。
今、r n という形の数列が、フィボナッチ数列を決める(5)式を満たすとしてみよう。すると、
rn+2 = rn+1 + rn ・・・(6)
が成り立つはずだ。rn で割っておくと
r2 = r + 1 ・・・(6)’
となり、これは黄金比を求めた(2)式と同じだ。そこで、黄金比となる解を φ、もう一方を ψ としておこう。つまり、
φ=( 1 + √5 ) / 2 、 ψ=( 1 - √5 ) / 2
これはどちらも(6)式を満たすので、
φn+2 = φn+1 + φn 、 ψn+2 = ψn+1 + ψn
が成り立っている。だから、c、d を定数として、
c φn + d ψn
も(6)すなわち(5)式を満たしている。フィボナッチ数列の最初の 2 項はともに1なので、この条件から c と d を決めよう。n=1、n=2で
c φ + d ψ = 1 、 c φ2 + d ψ2 = 1
ここで、φ2 = φ + 1、ψ2 = ψ+ 1が成り立っているので、2 乗の項を消去すると、上の 2式から
c + d = 0
が得られる。よって、
( 1 = ) F1 = c φ + dψ = cφ- cψ= c√5 、よって、c = 1 / √5
と決まる。さらに
ψ= ( 1 - √5 ) / 2 = -1 / φ
の関係に気づけば、フィボナッチ数は黄金比を用いて、
Fn = ( φn -(-1 / φ)n ) / √5
と書けてしまう。n を十分大きくとると、( 1 / φ ) n → 0 となるので、Fn ≒ φn / √5になる。こうして、
Fn+1 / Fn -(n大きいとき)→ φ
が得られる。これが、隣り合うフィボナッチ数の比が、だんだん黄金比に近づいてくる理由だ。
黄金比の話からフィボナッチ数列まで来てしまった。最後に、95 回で見た「パスカルの三角形」にもフィボナッチ数列が現れることを見ておしまいにしておこう。図の矢印の並びの数を足すとフィボナッチ数列が現れる。

フィボナッチはイタリアのピサで生まれた。「ピサのレオナルド」が名前の様だが、「ボナッチオ ( Bonacci o) の息子」、filius Bonacci と呼ばれていたようだ。filius が息子。フランス語では fils だ。filius はラテン語そのまま、イタリア語になっている。
イタリアのフィレンツェで国際会議が行われたときに参加したが、学会の合間にエクスカージョン(遠足)があり、ピサに行った。ピサの斜塔に上がり、ガリレオが振り子の等時性を発見した教会に行き、と定番コースの観光をしている最中に、数学の研究所を見つけた。Laboratorio FIBONACCI という名の研究所であった。

98.ブランコ
ブランコ、児童公園なんかに備えられているあれだ。
ブランコの存在は、古くは紀元前2000年より以前に遡るらしい。メソポタミア文明、今のシリアあたりのシュメールだ。もとはどうやら、宗教儀礼、特に豊穣祈願で使われていたらしい。葡萄が生産される地方では、ブランコを漕ぐことは葡萄の豊作を祈願した宗教儀式だったそうだ。葡萄の房が揺れるのと、ブランコが揺れるのと、連想したのかもしれない。
ロシアでは亜麻の豊作を、タイでは稲の豊作を祈願するため、ブランコを漕いでいたそうで、世界中に広まっている。高く漕ぐほど農作物は良く成長すると考えれていた。
中国ではブランコのことを鞦韆(しゅうせん)と呼ぶ。冬至の頃にブランコを漕いで、太陽の復活を願ったようだ。
朝鮮半島にも伝わる。春、旧暦5月、田植えの頃、田植えは主に女性が行っていた。そのとき、女性はブランコを漕ぐ。やはり豊作祈願だ。と同時に、働く女性の邪気払いのため、菖蒲を飾った端午の節句を行っていたようだ。だから、もともと端午の節句は、男の子のためのものではなくて、女性のためのものだった。
奈良時代くらいには日本に入ってきて、鎌倉時代には武士が抜鈎する世の中になったので、菖蒲の読みから「尚武」が連想され、男の子の節句になって、現在まで続いている。でも、ブランコを5月の端午の節句に漕ぐ朝鮮半島の影響か、俳句の世界では、鞦韆は春の季語に分類されている。
ブランコの語源は諸説あるようだが、おそらく、ポルトガル語のバランソ、balançoだろう。ポルトガル語でブランコのこともさすが、英語で言うところのバランスでもある。また、ポルトガル語-英語辞書を見ると、swing とも書いてあるので、まさにブランコが揺れることに応じている。
ところで。
授業で振動での共鳴現象の話をする。強制振動の運動方程式を解いてみせるのだが、現象としてはブランコを漕いでいるときに後ろから押して貰う場合が挙げられる。
しかし、人に押して貰う手伝いなしにブランコは漕げる。良く学生さんが勘違いするので、ブランコを一人で漕げるのはパラメータ共鳴という現象であることを説明するが、数式を使うと時間がかかるので、たいがい省略する。
微分の計算をしないといけないので厄介だが、一応ここに残しておこう。
振動の運動方程式は、振動する物体の座標をq(t) として
d2 q(t) / dt2 + ω2 q(t) = 0 ・・・(1)
となる。微分を知らない方は読み飛ばして貰おう。tは時間変数。この微分方程式の解は
q(t) = A sin ωt + B cos ωt
となる。AとBは積分定数。三角関数のかたちで振動する解だ。振り子の場合、ωと書いた“角振動数”は、振り子の紐の長さをl、重力加速度をgとして
ω=√(g / l )
となっている。振り子の時はq(t) は、鉛直方向とブランコの紐(鎖?)の為す角度となる。
今度はωが時間tに依存している場合を考える。振り子の場合、ひもの長さlが周期的に時間変化するとしよう。l0 を基準の紐の長さとして、その周りに周期的に伸び縮みするとしておこう。
l = l(t) = l0 ( 1-h cos γt )
h は1に比べて小さいとして、( 1-x )-1 ≒ 1 + x +・・・という展開式を用いると
ω(t)2 = g / l(t) ≒ g / l0 ×( 1 - h cos γt ) -1 = ω02 ( 1 + h cos γt )
となる。ここで、定数として、ω0 = √(g / l0 ) を定義した。運動方程式(1)は
d2 q(t) / dt2 + ω02 ( 1 + h cos γt ) q(t) = 0 ・・・(2)
と書き直せる。これを近似的にでも解くのは大変なので授業では省略してしまう。詳しい分析では、ひもの基準の長さl0 を周期的に変化させるときの角振動数γが、基準の振り子の角振動数ω0 と
γ= 2ω0 / n (nは自然数)
の関係にあるときに共鳴現象が起きることが知られている。n = 1 の時に特に大きな共鳴が得られるので、ここではその場合に限ろう。こうして
γ= 2ω0 + ε
とおいてみる。εは小さな量とする。だって、ブランコを漕ぐときに、そんなにうまく自分でコントロールする角振動数γを、ブランコの固有の角振動数ω0 にあわせられないんだから、ずれを入れておいて、でもまぁ、ずれは小さいとしておこうというわけだ。
こうして、運動方程式はさらに書き直せて
d2 q(t) / dt2 + ω02 ( 1 + h cos [ ( 2ω0 + ε)t ] ) q(t) = 0 ・・・(3)
になる。
解q(t) を
q(t) = a(t) cos[ (ω0 +ε/ 2 ) t ] + b(t) sin[ (ω0 +ε/ 2 ) t ] ・・・(4)
とおいて、運動方程式(3)に代入してみよう。ここで、aとbの時間微分、da(t) / dt 、db(t) / dt が小さな量εと同じ程度の量だとする。そして、aとbの時間についての2階微分、d2a(t) / dt2 、d2b(t) / dt2 はεの2乗ほど小さいとして無視する。さらに、運動方程式に代入した場合、cos[ 3(ω0 +ε/ 2 ) t ] や sin[3 (ω0 +ε/ 2 ) t ] の項が出てくるのだが、これらは小さい量hの2乗程度になることがわかっていて、これらも無視しよう。この項まで考慮するには最初に仮定した解q(t)にもcos[ 3(ω0 +ε/ 2 ) t ] や sin[3 (ω0 +ε/ 2 ) t ] の項を入れておく必要がある。ここではεもhも1次の項まで考慮する近似を取っているとして、出てきたcos[ 3(ω0 +ε/ 2 ) t ] や sin[3 (ω0 +ε/ 2 ) t ] の項を無視してしまう近似を使う。そうすると、途中の計算は全部端折って、(4)を(3)に代入した方程式から近似的に
-ω0 ( 2 da(t) / dt +b(t)ε+ ω0 h b(t) / 2 ) sin[ (ω0 + ε/ 2 ) t ]
+ω0 ( 2 db(t) / dt -a(t)ε+ ω0 h a(t) / 2 ) cos[ (ω0 + ε/ 2 ) t ] ≒ 0
という式が得られる。すべての時間tでこの式が成り立つためには
2 da(t) / dt +b(t)ε+ ω0 h b(t) / 2 = 0
2 db(t) / dt -a(t)ε+ ω0 h a(t) / 2 = 0
の2式が成り立っていればよい。さらに、a0 、b0 を時間に依存しない定数としてa(t)、b(t)を、
a(t) = a0 est 、b(t) = b0 est
とおいて、上の2式に代入してからest で割っておくと、ついでに2でも割っておくと
s a + bε/ 2 +ω0 h b / 4 = 0
s b - aε/ 2 +ω0 h a / 4 = 0
が得られる。最近の高校生は数学で行列を習わないと聞くが、行列とベクトルで上の2式を一発で表すと(といっても、ここでは書けないのだが・・・)
Γ s ( ε +ω0 h / 2 ) / 2 〕 |a|= |0|
L -( ε-ω0 h / 2 ) / 2 s 」 |b|= |0|
みたいに書ける(苦しい)。
a = 0、b = 0以外の解を持つには、行列の行列式が0であれば良いので、行列式を0とすると
s2 + ( ε2 -ω02 h2 / 4 ) / 4 = 0
が得られる。こうして、
s =( 1 / 2 )× √( (ω0 h / 2 )2 -ε2 ) ・・・(5)
が出てくる。結局、近似的ではあるが、q(t) が求まり、
q(t) = a0 est cos[ (ω0 +ε/ 2 ) t ] + b0 est sin[ (ω0 +ε/ 2 ) t ]
が得られる。sが純虚数、つまり(5)式で、
(ω0 h / 2 )2 -ε2 < 0
のときはei|s|t = cos (|s|t) +i sin (|s|t) だから、やっぱり振動する解になるので、共鳴は起きない。ところが
(ω0 h / 2 )2 -ε2 > 0 ・・・(6)
のときにはsは実数なので、解q(t) は時間tが経つと、est でどんどん大きくなる。ブランコだったら、振れる角度q(t)が時間とともにどんどん大きくなるということなので、漕げているというわけだ。
ブランコを漕いでどんどんブランコの振れ幅が大きくなるためには、(6)の条件から、角振動数の2ω0からのずれεが
-hω0 / 2 < ε< hω0 / 2
の範囲に収まっていれば共鳴が起きてブランコが漕げるというわけだ。
では、ブランコで“ひも”の長さをどう変化させれば良いのか?
ここで言う“振り子の紐の長さ”は、支点から重心までの長さと思えばよいので、ブランコを漕ぐときであれば紐の支点から重心の高さまでが“振り子の紐の長さ”とみなせる。重心の高さを変えるために、ブランコを立ち漕ぐするときであれば、体を伸ばしたり縮めたりするわけだ。ブランコが行って帰ってくるまでの周期Tは角振動数ω0に反比例、すなわちT = 2π/ ω0 だ。だから、ブランコが一周期する間に、体の上下動を2回することになる。だって、体の上下の一周期は2π/ γ= 2π / 2ω0 = T / 2だから、ブランコの一周期の半分で上下動を1回すれば“パラメータ共鳴”してブランコが漕げるというわけだ。ブランコの一周期であれば体の上下動は2回。こうして、ブランコが最高点に達した時に体を伸ばし、最低点を通過するときに体をかがめて縮め、次の最高点でまた体を伸ばす。この繰り返しでブランコは漕げる。
座ってブランコを漕ぐときには、最高点ではて膝から下の足を曲げて胴体と垂直方向に伸ばして重心を上げ、最低点では足を普通にぶらんと下の方に垂らして重心を下げ、次の最高点ではまた胴体と垂直方向に伸ばして重心を上げて、ブランコの半周期で1回の重心の上下動を行う。
おそらく立漕ぎでの重心の移動のほうが、座って漕ぐ場合の重心の上下移動より大きいだろう。だから、立漕ぎした方が、若干hが座り漕ぎの時より大きい。εが同じだと、hが大きい方がsが大きくなるので、est の割合で増大する振幅は、同じ時間tだけ漕いでいても立漕ぎの方が大きくなるというわけだ。
97.ライプニッツの積分法
ニュートンとは独立に、微積分法はライプニッツによっても発見されている。ニュートンによる積分法を説明したのに、ライプニッツに触れないのは片手落ちの様な気がするので、ライプニッツによる求積(積分)法を記しておこう。
ライプニッツは、ある曲線の下の( x 軸と囲まれた)面積を、“等しい長さ(横幅)の縦座標の総和”とみなした。これが積分だ。逆に、“縦座標と横座標それぞれの値の差が小さくなっていくときに、それらの比によって、曲線の接線が決まる”ことに気づいた。これが微分だ。
1675 年のノートによって、積分を見ておこう。

図で、曲線の下の OAB の面積は、縦座標 y の総和と見なした。“すべて”というラテン語の形容詞、omnis の属格、“すべての”に対応するomnium から、y の総和を
omn. y ( OAB の面積) ・・・(1)
と書いた。
一方、OBC は、面積 xw の長方形の総和だ。ここで、w は、横座標 x が幅 1 隣に進んだ時の y の増分だ。x+1 と x での y の差のこと。そこで、OBC の面積は、
omn.xw ( OBC の面積) ・・・(2)
と書ける。また、OA の長さを、ult.x と書き、OC の長さは w の総和、omn.w なので、長方形 OABC の面積は
ult.x , omn.w (長方形OABCの面積) ・・・(3)
と書く。ここで、コンマ( , )は、掛け算(×)の意味で使われている。こうして、(1)、(2)、(3)から、面積の関係として
ult.x , omn. w = omn.y + omn.xw
が得られる。ここで、右辺の y は、w の総和なので、
y = omn.w
と書けるので、これを代入すると
ult.x , omn.w = omn.omn.w + omn.xw
すなわち、
omn.xw = ult.x , omn.w -omn.omn.w ・・・(4)
と書き直される。
さて、まずは、
y = x
の曲線(直線)を考えよう。このときには、
y = omn.w = x
で、x が 1 単位進むと、y は 1 増えるので、w = 1 だ。したがって、(4)から、ult. x = xと書いて、
omn.x = x2 -omn.x
が得られる。整理すると
omn.x = x2 / 2
となる。要するに、y = x の曲線の下の面積は、x2 / 2 であるということで、y = x を x について積分したことになっている。
次いで、今度は、
w = x
としよう。(4)は
omn.x2 = x × omn.x - omn.omn.x
となるが、omn.x = x2 / 2 を先ほど求めたのでこれを代入すると
omn. x2 = x3 / 2 - omn.x2 / 2
となり、整理して、
omn.x2 = x3 / 3
が得られる。y = x2 の曲線の下の面積が x3 / 3 というわけで、y= x2 を x について積分したことになっている。
次は w = x2 といった具合にこの操作を繰り返していくことで、結局
omn.x n = xn+1 / (n+1)
が得られる。y= x n を x について積分したものは、 xn+1 / (n+1) となるということ。
ライプニッツが最初に使った記号、omn.は、ラテン語で総和を意味する summa omnium から来ている。omnium は先ほど記した、「すべての」の意味であり、summa は「和」のことだ。英語に入って、sum になる。ライプニッツは、最初用いていたomn. の代わりに、summa の頭文字の s を引き延ばして長くしたものを、新たに積分の記号にした。∫ だ。曲線 y ( = y(x) )の下の面積を、∫ y と書き、さらに後になって ∫ y dx と書くようになった。現在の記法だ。
微分は、“逆求積”であり、
∫ ℓ = ya としたときに ℓ を求める
演算とした。右辺は“面積”ということで、2つの変数の積でわざわざ書いている。ライプニッツは、積分も微分も“演算”としてとらえていて記法を生み出した。一方ニュートンは、積分は、x' = f (t) を x について解く“問題”と捉えていたようだ。
ちなみに、ライプニッツが最初に使ったラテン語の omnis であるが、「すべての」という属格が omnium であり、「すべてのために」という与格が、omnibus (オムニバス)だ。そこで、「すべての人のため」にあった乗合馬車のことが omnibus と呼ばれ、その後、馬車から自動車になり、やがて、omnibus が略されて bus になった。
通りを走っているバスって、ラテン語の変化する語尾じゃないか。
さらに、複数の独立した作品を一つに纏めた映画なんかを、オムニバス作品と呼ぶようになり、現在、大学で一つの講義を複数教員が行う授業形態を、オムニバスと呼んでいる。
オムニバス授業の準備をそろそろせねば・・・。
96.ニュートンの流率法
物理の授業をしていると、どうして微分や積分が物理に出てくるんだ、という文句が学生さんからよく出てくる。
でもね、力学の問題を解くために微分積分が生み出されたんだから仕方がない。
ライプニッツも同時期に微分積分学を考案していたものの、ニュートンは、力学の問題を扱うところから微分積分学を生み出した。力学は質点の運動の記述が大元にあるが、質点は運動しているので、もともと動的なものである。質点の運動の軌跡は、動点が辿る軌跡だ。平面曲線を考えると、平面はxとyの座標で表されるとすると、平面上の曲線は、ある関数 f(x,y)=0 で表される曲線に他ならない。例えば、半径 a の円は、f(x,y) =x 2 + y2 -a2 = 0 を満たす曲線だ。これを、点 (x,y) が“時間”とともに動いていった軌跡と考えるというわけだ。幾何学的に「原点からの距離 a が一定の点の集合」としてではなく、「動点が曲率一定(曲がり具合一定)で動いていった時の軌跡」を『円』と捉えるようなものだ。
動点が動いていく割合を、ニュートンは、「流率的速さ」あるいは単に「流率」と呼んでいた。そこで、ニュートン流の微分積分学は「流率法」と呼ばれる。
2次元平面で、“流量” x、 y の“流率”を、x'、y' と書くことにしよう。本当は x の上に黒丸・(ドット)を付けて書くのだが、フォントが無いので、代わりにダッシュを付けておこう。
こうして、各瞬間に描く無限に小さな線分の長さは速さに比例することから、O を“瞬間的時間”、x'、y' を x、y の流率(的速さ)として、ある瞬間に x、y であった長さは、次の瞬間には x + x'O、y + y'O になることが分かる。
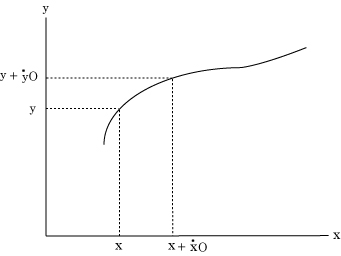
動点の曲線は f(x,y) = 0 で表されているので、
f(x,y) = 0
f(x+x'O, y+y'O) = 0
はともに曲線上にあるので、これらを連立させる。こうして、接線の傾きは、y 方向に動いた距離を、x 方向に動いた距離で割り算すれば得られるので、
y'O / x'O = y'/x'
として得られる。
具体的にやってみよう。
f(x,y) = x4 -ax2 -y
としてみる。f(x,y) = 0 の曲線とは、
y= x4 -ax2 ・・・(1)
のことだ。ここで、f(x+x'O, y+y'O) = 0でもあるので、代入して
f(x+x'O, y+y'O) = ( x+x'O)4 -a(x+x'O)2 -(y+y'O)
= 4x3 x'O-2axx'O-y'O+( O2 の項)+( O3 の項)+( O4 の項)
= 0 ・・・(2)
だ。ここで、(1)を使った。O は“瞬間的時間”であり小さいので、O2 、O3 、 O4 の項は小さいので無視しておき、(2)の両辺を O で割る。(2)の両辺を O で割ってから、残った O は小さいので無視すると言った方が良い。とりあえずやってみると、
4x3 x'-2axx'-y' = 0 、すなわち、y'/ x' = 4x3 -2ax
が得られる。この y' / x' が、点 (x,y) での曲線 f(x,y) = 0 の接線の傾きだ。これは今で言うところの、y を x で微分して得られる微係数を求めたことに他ならない。
では、微分の逆はどうだろうか。
1669 年にニュートンは、曲線の“下”の部分の面積、すなわち、曲線と x 軸に囲まれた面積を求める3つの規則を与えた。その内の「規則1」を見ておこう。規則1は
『もし、y = axm/n であれば、n / (m+n) × ax(m+n)/n が領域 ABC の面積に等しい』
というものだ。証明は「例から明らかである」と言って、ニュートンは6つの具体例を与えている。そのうちの一つが
「面積 S が、S = (2/3) × x3/2 となる曲線は?」
というものだ。ちょっと見ておこう。

図で、AB' の長さを x+O としておこう。AB の長さを x とするので、BB' の長さは Oだ。ただし、O は微小とする。今、長方形 BPQB' の面積が BCC'B' の面積と等しくなるように線分 PQ を引いたとする。BP の長さを v としよう。面積 S が S = (2/3) × x3/2 なので、両辺を 2 乗しておいて、
S2 = (4/9) x3 ・・・(2)
としておく。x が x から x+O に進んだ時の面積の増分は長方形 BPQB' の面積と等しいというのだから、BPQB' の面積は O×v より
(S + Ov )2 = (4/9) (x + O )3
が成り立っている。両辺展開しよう。
S2 +2SvO + v2O2 = (4/9) × (x3 +3x2O + 3xO2 +O3)
ここで、(2)から、S2 = (4/9) x3 であることを用いてから O で割ると
2Sv + v2O = (4/9) × (3x2 + 3xO +O2)
が得られる。ここでニュートンは
『もし BB' が無限に小さい、つまり O が零であると仮定すると、O がかかって
いる項は消え、かつ v は y に等しくなるので
2Sy = (4/9) 3x2 、すなわち y = x1/2
に還元される( S = (2/3) x3/2 を用いた)。』
として、問題を解いた。つまり、
『 y = x1/2 の曲線の下の面積( x 軸と囲む面積)は、S = (2/3) x3/2 である』
ここで、S = (2/3) x3/2 = 2 / (1+2) x(1+2)/2 であるので、ニュートンは
『S = n / (m+n) × ax(m+n)/n を取り上げ、面積 S を与える曲線は y = axm/n であ
ることを証明する予定である』
とした。この証明は簡単で、両辺 n 乗してから、上でやったことと同じことをすればできる。どうも、ニュートンは書き残していないようだが。
積分法の発見だ。1669 年、おそらく 1664 年から 1666 年の間に、ニュートンによる。
95.パスカルの三角形からニュートンへ
nを自然数として、( x + y )n の展開は比較的容易にできるが、逆の因数分解はなかなか難しい。
高校生になった息子が、
x4 + 4 y4 を因数分解せよ
という問題に出くわし、どうしたらよいかわからないようだった。
物理の研究を30年近くしている身にも、こんなに綺麗な数式を、なぜわざわざ因数分解するのか?という疑問を持つが、練習問題だから仕方がない。
結局息子は自分で解いたが、答えは
x4 + 4 y4 = ( x2 +2 x y + 2 y2 ) ( x2 -2 x y + 2 y2 )
左辺と右辺のどちらが美しいか?
でも、そんなこといったら、i = √(-1) という、2乗したらー1になる、つまり i 2
= -1 になる虚数単位を使えば
x4 + 4 y4 = ( x2 + i 2 y2 ) ( x2 - i 2 y2 )
= ( x + √2 i3/2 y ) ( x-√2 i 3/2 y ) ( x-√2 i 1/2 y ) ( x+√2 i 1/2 y )
= ( x + √2 ei(3/4)π y ) ( x-√2 ei(3/4)πy ) ( x-√2 ei(1/4)πy ) ( x+√2 ei(1/4)πy )
ともできるぞ?ここで、i 3/2 = ei(3/4)π =(-1 + i ) / √2、また、 i 3/2 = ei(1/4)π =(1 + i ) / √2
だ。
( 1 + x )n を展開した時の係数を、2項係数と呼ぶ。1665年、二項定理に現れる二項係数が、パスカルの三角形として簡単に表された。二項定理は
( 1 + x ) = 1 + x
( 1 + x )2 = 1 + 2 x + x2
( 1 + x )3 = 1 + 3 x + 3 x2 + x3
( 1 + x )4 = 1 + 4 x + 6 x2 +4 x3 + x4
・・・・
( 1 + x )n = nC0 + nC1 x + nC2 x2 + ・・・ + nCn xn
ただし nCr = n(n-1)×・・・×(n-r+1) / (1・2・3×・・・×r)
となる。ここで、xr の係数を並べると
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
・・・・・・・・・・・・
と三角形に並ぶが、中の数字は必ず、上斜め右と上斜め左の数の和になっている。例えば 5 段目の 6 は、右斜め上の 3 と左斜め上の 3 を足した数になっている。これをパスカルの三角形と言う。
少し並べ替えて、(1 + x )n の係数を縦に並べよう。一番上の段は、n の値。
|
n=0 |
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
1 |
3 |
6 |
10 |
|
|
|
|
1 |
4 |
10 |
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
1 |
そうすると、右へ右へ新たな数字を書き込むには、左斜め上と左の数字を足していけば良いことが見て取れる。たとえば、n = 5 の 3 段目の 10 は、左斜め上の 4 と左の 6 を足したものだ。空欄は 0 と思う。
ニュートンは、この表を、n が負の時に拡張した。一番上の段は、n の値。
|
-5 |
-4 |
-3 |
-2 |
-1 |
n=0 |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
← x0 |
|
-5 |
-4 |
-3 |
-2 |
-1 |
|
1 |
2 |
3 |
4 |
5 |
← x1 |
|
15 |
10 |
6 |
3 |
1 |
|
|
1 |
3 |
6 |
10 |
← x2 |
|
-35 |
-20 |
-10 |
-4 |
-1 |
|
|
|
1 |
4 |
10 |
← x3 |
|
70 |
35 |
15 |
5 |
1 |
|
|
|
|
1 |
5 |
← x4 |
|
-126 |
-56 |
-21 |
-6 |
-1 |
|
|
|
|
|
1 |
← x5 |
|
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
|
|
|
|
|
|
|
表は下へ、無限に続く。n が負の時の表の作り方は、右隣の数字から真上の数字を引くことで得られる。例えば、n = -3 の時の4段目、x3 の係数になる-10 は、右隣の-4 から真上の 6 を引く、つまり、-4-6 = -10 として得られる。こうして、n ≧ 0 のパスカルの三角形から、n が負の左側へ表を拡張していく。こうすると、例えば、n =-3をみていくと、確かに
( 1 + x )-3 = 1 - 3 x + 6 x2 - 10 x3 + 15 x4 -21 x5 +・・・
と、無限に続く二項展開が得られる。微分積分学を学んでテーラー展開を知っている人は、x = 0 の周りのテーラー展開をしてみるとよい。
1676 年には、ニュートンは、n が分数の場合の展開にも成功する。ただし、パスカルの三角形を直接拡張したものではないことを、1676 年の手紙で示している。( 1-x2 )n 、(n=0,1,2・・・) のグラフの下の面積を求める問題から、n = 1 / 2 の場合への補間を考えて得たそうだ。ニュートンが書いたように書くと(下付き棒線は本当は上に書いている、また分数は分数として書いている)
P +PQ |m/n
= P m/n + (m / n ) AQ + ( m-n ) / (2n) BQ + (m-2n) / (3n) CQ + (m-3n) / (4n) DQ +&c
ここで、P は第1項、Q は残りの項を P で割ったもの、A、B、C、D はすぐ前の項といったことだ。
具体例を見ておこう。( 1 + x ) 1/2 でやってみよう。1 + x の平方根だ。見比べると P = 1、Q = x、m = 1、n = 2 だ。A は前の項、Pm/n = 1 、B も前の項、(m/n)AQ =(1/2)×1×x、C も前の項、(m-n) / (2n) BQ = (1-2) / (2×2) ×(x/2) × xだ。こうして、
( 1 + x )1/2 = 1 + (1/2) x -(1/8) x2 + (1/16) x3 -(5/128)x4 +・・・
となることが確かめられる。これも、テーラー展開を知っていると確認できる。
94.゛機械学的”方法による求積
新学期が始まり、いつも2~3週間したら、黄金週間という名の連休が入る。今年、2019年は改元があり、10連休になった。
ずっと以前、大学に着任してまだ 5 年ほど、助手の頃に、共通教育という名の一般教育の授業で、「数学と物理学の進歩」だったか、「物理学の進歩と数学」だったかという名の授業を持つことになった。こういう科目は、ベテランの方が広い教養を活かしてお引き受け頂ければよいのだが、そういう発想がないのか、ようやらんのか、何故か私に回ってきた。
そこで、ネタ作りで、いろいろ調べた。もちろん、ニュートン力学と微積分や、一般相対論とリーマン幾何は話そうと思ったが、それだけだと話が広がらないので、沢山の本を読んだりして知識を集める。自分で講義ノートを作って板書しただけなので、すでに 20 年近くたってしまって講義ノートが散逸気味だ。そこで、残っている講義ノートをもとに備忘しておこう。
ニュートンやライプニッツの積分に行く前に、古来からの求積法を調べる。
そこで出くわしたものの一つが、アルキメデスの「方法」に書かれているという、放物弓型の面積の計算法だった。
図の太線で書かれた放物線に 2 点、A と C をとる。線分 AC に平行な放物線の接線を引き、接線が放物線に接する点を B とする。そうすると、放物線と線分 AC で囲まれた放物弓型の面積は、三角形 ABC の面積の 3 分の 4 倍に等しい。アルキメデスは、「てこの原理」を用いて示す。
まず、線分 AC の中点をとり、D とする。D と B を結ぶ直線を描く。D を通って放物線の焦点と頂点を結ぶ線分に平行な軸を引いたと考えても良い。その軸と放物線との交点が B だ。
次に、点 C で、放物線の接線を引き、線分 DB を延長した直線との交点を E とする。また、点 A から DB に平行に引いた直線が、点 C での接線と交わる点を F とする。三角形の辺 BC を延長して線分 AF と交わる点を K とする。さらに、CK を延長して、線分の長さが CK = KH となるように、点 H を取る。
さらに、直線 CK 上に勝手な点 N をとり、N を通り線分と DB と平行な直線を引く。この直線が CF と交わる点を M、CA と交わる点を O、放物線との交点を P とする。図の通り。

ここから、少し放物線の性質を使わせてもらう。
放物線の性質から、それぞれの線分の長さに関係がつけられる。まず、
EB = BD
これを使うと、三角形 CED と三角形 CMO が相似であることから、
MN = NO
が言える。
もう一度、放物線の性質を使わせてもらおう。
MO : OP = CA : AO
という比が、放物線であるということで得られる。これを使うと、三角形 CNO と三角形 CKA が相似であることから
MO : OP = CA : AO =CK : KN =HK : KN
が得られる。最初の等式は放物線の性質、2 番目は三角形の相似、3 番目は CK = HK と線分の長さをとって作図したことによる。第 1 式と第 4 式を取り出して書いておくと
MO : OP = HK : KN
になる。分数で書けば
MO / OP = HK / KN
だから、
MO × KN = OP × HK ・・・(1)
ということだ。
さて、ここからが機械学的だ。
まず、線分 CH を、点 Kを 釣り合いの中心とした“てこ”の棒と考える。また、OP と等しい長さの線分 TG を、その中心が H に来るように置く。図の通り。そうすると、(1)式は
MO × KN = TG × HK ・・・(2)
と書き直せる。ここで、てこ、またはシーソーの支点を K とし、MO と TG の線分が一様密度の棒と考えると、(2)式は、(重さ)×(てこの腕の長さ)が左右両辺で等しいという式になっている。左辺は、支点からの距離 KNに 、重さ MO を置いた式、右辺は支点からの距離 HK に重さ TG を置いたものと考えると、両者は釣り合っているという式だ。シーソーの釣り合いについては第 38 回参照。
N は勝手な点として CK 上に取ったので、この操作を点 N を CK 上を動かしていって、今までの操作を繰り返すと、放物弓型を構成する線分 OP を全部 1 点 H に集めたものと、線分 MO をその線分が置かれている各点での位置 N ごとにすべて集めたもの、すなわち三角形 FAC が釣り合うことになる。三角形 FAC を構成する線分は各点 Nごとに場所は異なっておかれているが、その重さを三角形の重心にすべて集めたものと同じになるので、三角形 FAC の面積に対応した重さを、三角形 FAC の重心においたと思えばよい。それが、放物弓型の面積に対応した重さと、支点 K で釣り合うというわけだ。三角形 FAC の重心は、線分 CK を 2 対 1 に内分する点、図では W であるので、
(放物弓型の重さ)× HK = (三角形FACの重さ)× KW ・・・(3)
となる。また
3 × KW = CK =HK ・・・(4)
である。W は CK を 2 対 1 に内分していることと、作図から CK = HK だったことを使った。さらに、最初の設定から
AC = 2 × AD
であったので、三角形の相似を睨んで
AK = 2 × DB
となり、結果、
AF = 2 × AK = 4 × DB
となるので、
(三角形FACの面積)=4 ×(三角形ABCの面積) ・・・(5)
となることが分かる。底辺 AC が共通で、高さ AF と DB が 4 倍違うからだ。
こうして、(3)の KW を(4)で HK にして、また三角形 FAC を(5)を使って三角形 ABC に置き換えると
(放物弓型の重さ)× HK = (三角形FACの重さ)× KW
= 4 ×(三角形ABCの重さ)× HK / 3
なので、重さと面積が比例していることから
(放物弓型の面積)= ( 4 / 3 ) ×(三角形ABCの面積)
が得られる。
確かに、放物線と線分 AC で囲まれた放物弓型の面積は、三角形 ABC の面積の 3 分の 4 陪に等しいことが言えた。
面積を求める際に、物理のてこの原理を使うとは、さすがアルキメデス。「支点とてこを与えられたら地球を動かして見せよう」と言っただけのことはある。
93.授時
第69回で、宇宙観の進展について備忘した。どうしても西洋中心の宇宙観になってしまうが、中国ももちろん古くから進んでいた。
初期中国では、宇宙の空間的構造としては 3 つの説が唱えられていた。1 つ目は天地は平面的とした蓋天(がいてん)説。天と地は平行であり、離れた2点から太陽の高度を図り、天の高さは 80,000 中国里、多分およそ 5,700 kmと見積もっていた。後に天はお椀をかぶせた形に変更している。2 つ目は渾天(こんてん)説で、天界は鶏卵の殻の様に天球から成っていて、大地は鶏卵の黄身にあたるような宇宙の形だと考えた。3 つ目が宣夜(せんや)説で、宇宙は無限の虚空であり、天体は自由な空間に浮かんでいるとした。
西洋の天動説に近いのは 2 番目の渾天説だ。
キリスト紀元 78 年に生まれ、139 年に亡くなる中国、後漢時代の大科学者、宮廷天文官であった張衡(ちょうこう)は、渾天説に立っていたようだ。しかも、地球は宇宙に浮いた球体で、九大陸を持つと考えていた。彼は、それまでにあった天体観測用の天球儀を改良したうえで、天体観測を行って星々を記録していったようだ。それに飽き足らず、水力で動く天球儀を作り、締め切った部屋の中で水力により天球儀を回転させ、動く天球儀にあわせて、これこれの位置に今、何々の星が南中するはずだとか昇ってくるはずだとか指令を出し、部屋の外で観測している者が本当に、水力で動く天球儀の予言通りに星々が現れたりするか確認したところ、張衡の言う通りだったそうだ。
張衡はまた、地動儀、現在言うところの地震計を発明している。青銅でできた甕の周囲に 8 匹(8頭?)の龍がついていて、それぞれの口に青銅の球を加えており、地震が来て揺れを感じると、龍の口から球が落ち、下で待ち構えている青銅製の蛙の口に入るというようになっている。地震で落ちる球は 1 つで、これにより震源の方向も分かるらしい優れものだ。後漢書に、「一つの球が落ちたが感じる揺れは無かった。ところが、数日後に都にやってきた使者が、都から(今の距離で) 640 km 離れた場所で地震があったと伝えた」とあり、実際に機能していたようだ。

国立科学博物館、張衡「地動儀」の復元模型
張衡はまた、円周率πの値の計算も行っている。彼は、およそ3.16と与えた。後に、紀元 400 年代末、500 年より少し前に、祖沖之(そちゅうし)が、円に内接する正24,576 角形の辺の長さを計算し、それが円周の長さに近いものとして、円周率は3.1415926 と 3.1415927 の間だと結論づけている。西洋文明がこの結果を得るのは、紀元 1,600 年頃なので、この時点で 1,100 年くらい先んじていた。
さて、張衡は文人でもあり、例えば 6 世紀に編纂された「文選」に彼の「帰田賦」が収められている。後漢の安帝に召されるも、安帝は宦官の専横を許して政治が乱れ、次に宦官に擁立された順帝のときに職を辞して故郷に帰るときのことを謳った賦が帰田賦だ。というわけで、「都住まいも永くなるが、世の中を良くする助けもできず、川に臨んで魚を取ることを願い、河が清く澄む時世を未だ待つ」といった感じで始まる。政(まつりごと)は乱れている。
その文選であるが、清少納言の枕草子にも「書は、文集。文選、新賦。史記、五帝本紀。願文。表。博士の申文。」とあり、「書(ふみ)は白氏文集。文選、特に新賦が良い。(以下略)」と言っているので、公家の常識だったのだろう。遡って飛鳥から奈良時代の知識人である大伴旅人も、6 世紀に編まれた文選は当然知っていただろう。万葉集の梅花歌三十二首の序を書いた大伴旅人は大宰府に居てそれを編んだそうだが、何故太宰府かと言うと、当時権力を握っていた藤原四兄弟、武智麻呂(むちまろ)、房前(ふささき)、宇合(うまかい)、麻呂(まろ)に左遷されていたという説があるようだ。梅花歌が詠まれる前に、藤原四兄弟が無実の罪で長屋王を追い詰め自殺させるという長屋王の変が起きている。まつりごとは乱れていた。
もう、語り尽くされていることではあるが、備忘として記しておこう。
大伴旅人は、梅花歌序で「于時 初春令月 気淑風等和」と記す。「初春の麗しい月であり、気候も良く風は穏やかだ」と。これは、張衡の帰田賦の「於是仲春令月 時和気清」(これにおいて、春半ばの麗しい月、時節は和やかで、大気は澄んでいる)を踏まえているのだろう。梅花歌自体は花を愛でるような歌だが、大伴旅人は序を書くことで読者に張衡の帰田賦を想起させ、張衡が都を離れて故郷に帰らざるを得なかったと同じく、乱れた政治の世であることを意識させる装置を仕込んでおいたようだ(「「令和」から浮かび上がる大伴旅人のメッセージ」品田悦一(東京大学総合文化研究科教授))。さすが、万葉集の研究家。指摘は鋭い。
古代中国では、天子(皇帝)は天帝の天命を受けて「宇宙」、宇は空間、宙は時間のことであるが、これらを支配するものとされた。時間を支配する具体として、人民に暦を授けていた。暦作成のために天文官を置き、詳細な天体観測を行っていた面はある。これを観象授時と呼ぶ。支配者や王朝が変わった時には、新たに天命を受けたとして改暦を行う。天の命が革(あらた)まったときには王朝を倒す革命が起きるというわけだ。
張衡が亡くなってから 50 年後に、後漢の少帝が殺され、統治機能を失う。さらに 30年後に、後漢は滅び、魏、呉、蜀が並ぶ三国時代に入る。