101.レポート分析
学生さんにレポートを課すことが良くある。そして、曲者のレポートチェック。
最近の学生さんは真面目なのでそう云うことは無いのだが(と期待しているのだが)、長く教員をしていると、コピー・アンド・ペーストが散見されることがあった。物理学のレポートなので、ネットからのコピーでは解答に到達するのはなかなか難しいが、時折、物理の法則の内容などの論述を問題にして課すと、ネットからコピーしてきたものが見られることがあった。
別に、コピーを見破るソフトを使わなくても、文体を見れば大体わかる。
ひどいときは、複数のサイトから採ってきて繋いだと見えて、途中から文体が変わっていたこともあった。
もっとひどいときは、「ですます」調が「である」調に途中で変化している。
まぁ、御愛嬌なので、目くじらを立てないが。
物理の問題を解くといった課題のレポートで多いのは、誰かのレポートを見せてもらって引き写しているという代物だ。今でも念のために学生さんに言っているのだが、誰のレポートが大元で、それが誰の手に渡って次々にコピーされていったかの系統樹が書ける。これがなかなか楽しい。レポートされた内容はほぼ同じなので、どちらかのレポートが、誰かに見せてもらって作成されていることは解るのだが、どちらが元かも誤字の伝搬を見ていけばわかる。例えば、ギリシャ文字の ν(ニュー)のところが、伝搬していくうちにアルファベットの v(ヴイ)になっているという感じ。また、見せてもらった世代が後になるにつれ、誤字が増える。それで系統樹が書ける。
レポートといえども人に見てもらうのであるから、読ませる相手への贈り物であり、読んで欲しい相手に届く言葉使いと数式使いを心掛けてほしい。
何代か前の学長さんの卒業式の式辞が毎年ほぼ同じで、式辞の最後に、学生さんに贈る格言というか言葉だけを違えていたことがあった。まぁ、式辞だからそう変える必要もないのかもしれないが。
でも、まぁ、心がこもっていないなぁという感想を持ったのは確かだ。
そこで、挨拶とはどういうものか、具体例でみておこうと思った。すでにずっと前の卒業式の式辞は手に入らないので、折角だから最高に偉い人が行った格調高い挨拶で分析してみよう。
テキスト分析というのは、人文社会系の先生が得意とするものだが、理系の素人でもやってみよう。
このような偉い人の格調高い挨拶を読む機会もなかなか無いだろうから、全文を載せておこう。官邸のホームページに広く公開されているので、著作権の問題はなさそうだ。
某氏がおこなった、2019年8月6日広島市原爆死没者慰霊式並びに平和祈念式でのあいさつ。便宜上、各段落に番号を付けておく。
『(1.1) 今から74年前の今日、原子爆弾により、十数万ともいわれる貴い命が失われました。街は焦土と化し、人々の夢や明るい未来が容赦なく奪われました。一命をとりとめた方々にも、筆舌に尽くし難い苦難の日々をもたらしました。
(1.2) 原子爆弾の犠牲となられた数多くの方々の御霊(みたま)に対し、謹んで、哀悼の誠を捧(ささ)げます。
(1.3) そして、今なお被爆の後遺症に苦しまれている方々に、心からお見舞いを申し上げます。
(1.4) 核兵器によってもたらされた広島と長崎の悲劇を決して繰り返してはなりません。唯一の戦争被爆国として、「核兵器のない世界」の実現に向けた努力をたゆまず続けること。これは、令和の時代においても、変わることのない我が国の使命です。新しい時代を平和で希望に満ち溢(あふ)れた時代としなければなりません。
(1.5) 近年、世界的に安全保障環境は厳しさを増し、核軍縮をめぐっては各国の立場の隔たりが拡大しています。
(1.6) 我が国は、「核兵器のない世界」の実現に向け、非核三原則を堅持しつつ、被爆の悲惨な実相への理解を促進してまいります。核兵器国と非核兵器国の橋渡しに努め、双方の協力を得ながら対話を粘り強く促し、国際社会の取組を主導していく決意です。
(1.7) 明年は、核兵器不拡散条約(NPT)発効50周年という節目の年を迎え、5年に1度のNPT運用検討会議が開催されます。この会議において、意義ある成果を生み出すために、一昨年、ここ広島から始まった核軍縮に関する「賢人会議」の提言等を十分踏まえながら、各国に積極的に働きかけていく決意です。
(1.8) 私たちには、唯一の戦争被爆国として、核兵器の非人道性を、世代や国境を越えて伝え続ける務めがあります。
(1.9) 被爆者の方々から伝えられた被爆体験を、しっかりと、若い世代へと語り継いでいく。
(1.10) そして、広島や長崎を訪れる世界中の人々が、被爆の悲惨な実相に触れることで、平和への決意を新たにすることができる。そうした取組を我が国として、着実に推し進めてまいります。
(1.11) 被爆者の方々に対して、保健、医療、福祉にわたる支援の必要性をしっかりと受け止め、今後も、被爆者の方々に寄り添った援護施策を総合的に推進してまいります。特に、原爆症の認定について、引き続き、一日も早く結果をお知らせできるよう、できる限り迅速な審査を行ってまいります。
(1.12) 結びに、「国際平和文化都市」として発展を遂げた、ここ広島市において、「核兵器のない世界」と恒久平和の実現に向けて力を尽くすことをお誓い申し上げます。原子爆弾の犠牲となられた方々のご冥福と、ご遺族、被爆者の皆様、並びに、参列者、広島市民の皆様のご平安を祈念いたしまして、私の挨拶といたします。』
各段落の最初の1は、令和元年ということでつけた。全部で12段落。
このテキストと比較すべきは、まずは昨年同じ日に同じ場所で同じ人物により行われた挨拶だろう。
『(30.1) 一発の原子爆弾が、街を一瞬にして破壊し、十数万ともいわれる貴い命を奪いました。あれから73年、一命をとりとめた方々にも、筆舌に尽くし難い苦難の日々をもたらしました。若者の夢や明るい未来が容赦なく奪われました。
(30.2) 原子爆弾の犠牲となられた数多くの方々の御霊(みたま)に対し、謹んで、哀悼の誠を捧(ささ)げます。
(30.3) そして、今なお被爆の後遺症に苦しまれている方々に、心からお見舞いを申し上げます。
(30.4) 広島、長崎の悲劇を再び繰り返してはならない。唯一の戦争被爆国として、「核兵器のない世界」の実現に向けて、粘り強く努力を重ねていくこと。それは、我が国の使命です。
(30.5) 近年、核軍縮の進め方について、各国の考え方の違いが顕在化しています。
(30.6) 真に「核兵器のない世界」を実現するためには、被爆の悲惨な実相の正確な理解を出発点として、核兵器国と非核兵器国双方の協力を得ることが必要です。我が国は、非核三原則を堅持しつつ、粘り強く双方の橋渡しに努め、国際社会の取組を主導していく決意です。
(30.7) その具体的な取組として昨年、核軍縮に関する「賢人会議」を、ここ広島で開催しました。
(30.8) 「賢人会議」を通じて有識者の知見も得ながら、核兵器不拡散条約(NPT)発効50周年となる2020年のNPT運用検討会議が意義あるものとなるよう、積極的に貢献してまいります。
(30.9) また、その非人道性を、後の世に、また世界に、伝え続ける務めが我々にあります。
(30.10) 若い世代が、被爆者の方々から伝えられた被爆体験を語り継ぐ。
(30.11) 政府として、そうした取組をしっかりと推し進めてまいります。
(30.12) 被爆者の方々への援護施策については、保健、医療、福祉にわたる支援の必要性をしっかりと受け止め、被爆者の方々に寄り添いながら、今後とも、総合的に推進してまいります。特に、原爆症の認定について、引き続き、一日も早く結果をお知らせできるよう、できる限り迅速な審査を行ってまいります。
(30.13) 結びに、永遠の平和が祈られ続けている、ここ広島市において、「核兵器のない世界」と恒久平和の実現に向けて力を尽くすことをお誓い申し上げます。原子爆弾の犠牲となられた方々のご冥福と、ご遺族、被爆者の皆様、並びに、参列者、広島市民の皆様のご平安を祈念いたしまして、私の挨拶といたします。』
平成30年ということで、30をつけた。全部で13段落。
2つのテキストを見て行こう。
まず、(1.1)は(30.1)に対応している。若干の言いまわし、「命を奪いました」が「命が失われました」等の変更はあるが、ほぼ同じ内容である。
『(1.1) 今から74年前の今日、原子爆弾により、十数万ともいわれる貴い命が失われました。街は焦土と化し、人々の夢や明るい未来が容赦なく奪われました。一命をとりとめた方々にも、筆舌に尽くし難い苦難の日々をもたらしました。』
『(30.1) 一発の原子爆弾が、街を一瞬にして破壊し、十数万ともいわれる貴い命を奪いました。あれから73年、一命をとりとめた方々にも、筆舌に尽くし難い苦難の日々をもたらしました。若者の夢や明るい未来が容赦なく奪われました。』
(1.2)は(30.2)と全く同じ引き写しである。
(1.3)も(30.3)と全く同じ。
(1.4)は(30.4)と内容は同じである。「核兵器のない世界」の実現への希求だ。令和と元号が変わったので、それを入れたのみ。
『(1.4) 核兵器によってもたらされた広島と長崎の悲劇を決して繰り返してはなりません。唯一の戦争被爆国として、「核兵器のない世界」の実現に向けた努力をたゆまず続けること。これは、令和の時代においても、変わることのない我が国の使命です。新しい時代を平和で希望に満ち溢(あふ)れた時代としなければなりません。』
『(30.4) 広島、長崎の悲劇を再び繰り返してはならない。唯一の戦争被爆国として、「核兵器のない世界」の実現に向けて、粘り強く努力を重ねていくこと。それは、我が国の使命です。』
(1.5)は(30.5)と同一の内容。核軍縮について各国の「違いが顕在化」が「隔たりが拡大」へと事態は悪くなっているようだ。
『(1.5) 近年、世界的に安全保障環境は厳しさを増し、核軍縮をめぐっては各国の立場の隔たりが拡大しています。』
『(30.5) 近年、核軍縮の進め方について、各国の考え方の違いが顕在化しています。』
(1.6)は(30.6)に対応。核兵器保有国とそうでない国の「橋渡し」を行い、両者の「協力」を得る。表現内容の順番が変わったのみ。
『(1.6) 我が国は、「核兵器のない世界」の実現に向け、非核三原則を堅持しつつ、被爆の悲惨な実相への理解を促進してまいります。核兵器国と非核兵器国の橋渡しに努め、双方の協力を得ながら対話を粘り強く促し、国際社会の取組を主導していく決意です。』
『(30.6) 真に「核兵器のない世界」を実現するためには、被爆の悲惨な実相の正確な理解を出発点として、核兵器国と非核兵器国双方の協力を得ることが必要です。我が国は、非核三原則を堅持しつつ、粘り強く双方の橋渡しに努め、国際社会の取組を主導していく決意です。』
(1.7)は(30.7)と(30.8)を纏めている。2020年に核兵器不拡散条約発効50年の節目となることと、賢人会議の提言があったことを述べている。
『(1.7) 明年は、核兵器不拡散条約(NPT)発効50周年という節目の年を迎え、5年に1度のNPT運用検討会議が開催されます。この会議において、意義ある成果を生み出すために、一昨年、ここ広島から始まった核軍縮に関する「賢人会議」の提言等を十分踏まえながら、各国に積極的に働きかけていく決意です。』
『(30.7) その具体的な取組として昨年、核軍縮に関する「賢人会議」を、ここ広島で開催しました。(30.8) 「賢人会議」を通じて有識者の知見も得ながら、核兵器不拡散条約(NPT)発効50周年となる2020年のNPT運用検討会議が意義あるものとなるよう、積極的に貢献してまいります。』
(1.8)は(30.9)であり、核兵器の非人道性を伝える務めがあることを述べている。
『(1.8) 私たちには、唯一の戦争被爆国として、核兵器の非人道性を、世代や国境を越えて伝え続ける務めがあります。』
『(30.9) また、その非人道性を、後の世に、また世界に、伝え続ける務めが我々にあります。』
(1.9)は(30.10)の引き写しで、若い世代への被爆体験を語り継ぐことである。
『(1.9) 被爆者の方々から伝えられた被爆体験を、しっかりと、若い世代へと語り継いでいく。』
『(30.10) 若い世代が、被爆者の方々から伝えられた被爆体験を語り継ぐ。』
(1.10)は(30.11)に対応しているが、少し詳しくなっている。
『(1.10) そして、広島や長崎を訪れる世界中の人々が、被爆の悲惨な実相に触れることで、平和への決意を新たにすることができる。そうした取組を我が国として、着実に推し進めてまいります。』
『(30.11) 政府として、そうした取組をしっかりと推し進めてまいります。』
(1.11)は(30.12)とほぼ同様。被爆者の方達に対して具体性のない、内容の無いことを言っている。
『(1.11) 被爆者の方々に対して、保健、医療、福祉にわたる支援の必要性をしっかりと受け止め、今後も、被爆者の方々に寄り添った援護施策を総合的に推進してまいります。特に、原爆症の認定について、引き続き、一日も早く結果をお知らせできるよう、できる限り迅速な審査を行ってまいります。』
『(30.12) 被爆者の方々への援護施策については、保健、医療、福祉にわたる支援の必要性をしっかりと受け止め、被爆者の方々に寄り添いながら、今後とも、総合的に推進してまいります。特に、原爆症の認定について、引き続き、一日も早く結果をお知らせできるよう、できる限り迅速な審査を行ってまいります。』
(1.12)は(30.13)同様、結びの文章。『永遠の平和が祈られ続けている』が『「国際平和文化都市」として発展を遂げた』に代えられたのみ。
『(1.12) 結びに、「国際平和文化都市」として発展を遂げた、ここ広島市において、「核兵器のない世界」と恒久平和の実現に向けて力を尽くすことをお誓い申し上げます。原子爆弾の犠牲となられた方々のご冥福と、ご遺族、被爆者の皆様、並びに、参列者、広島市民の皆様のご平安を祈念いたしまして、私の挨拶といたします。』
『(30.13) 結びに、永遠の平和が祈られ続けている、ここ広島市において、「核兵器のない世界」と恒久平和の実現に向けて力を尽くすことをお誓い申し上げます。原子爆弾の犠牲となられた方々のご冥福と、ご遺族、被爆者の皆様、並びに、参列者、広島市民の皆様のご平安を祈念いたしまして、私の挨拶といたします。』
うーむ。構成も言い回しも、ほぼ同じ。まぁ、挨拶ってこんなものなんだろう。
でも、収穫があった。核軍縮について各国の考え方の「違いが顕在化」したのは昨年だが、今年は「隔たりが拡大」へと事態は悪い方向へ進んでいるというメッセージだ。
もうひとつ。上記以外は、昨年と今年でほとんど同じことを述べている。ということは、この1年で何もしていないということ、何の施策も実行していないということが読み取れる。
まさに、上っ面の言葉だけ。
では、2019年8月9日の長崎原爆犠牲者慰霊平和祈念式典での同一人物のあいさつを見ておこう。同じ式典ではないので、きっと違うはずだ。ちなみに、広島はウラン、長崎はプルトニウム型原爆が投下されている。米軍による、違う形式の核兵器使用の実験だ。
『(N.1) 本日、被爆74周年の長崎原爆犠牲者慰霊平和祈念式典に当たり、原子爆弾の犠牲となられた数多くの方々の御霊(みたま)に対し、謹んで、哀悼の誠を捧(ささ)げます。
(N.2) そして、今なお被爆の後遺症に苦しまれている方々に、心からお見舞いを申し上げます。
(N.3) 今から74年前の今日、一発の原子爆弾により、一瞬にして街は焦土と化し、7万ともいわれる貴い命が失われました。人々の夢や明るい未来が容赦なく奪われ、一命をとりとめた方々にも、筆舌に尽くし難い苦難の日々をもたらしました。
(N.4) 核兵器によってもたらされた長崎と広島の惨禍を決して繰り返してはなりません。唯一の戦争被爆国として、「核兵器のない世界」の実現に向けた努力をたゆまず続けること。これは、令和の時代においても、変わることのない我が国の使命です。新しい時代を平和で希望に満ち溢(あふ)れた時代としなければなりません。
(N.5) 近年、世界的に安全保障環境は厳しさを増し、核軍縮をめぐっては各国の立場の隔たりが拡大しています。
(N.6) 我が国は、「核兵器のない世界」の実現に向け、非核三原則を堅持しつつ、被爆の悲惨な実相への理解を促進してまいります。核兵器国と非核兵器国の橋渡しに努め、双方の協力を得ながら対話を粘り強く促し、国際社会の取組を主導していく決意です。
(N.7) 明年は、核兵器不拡散条約(NPT)発効50周年という節目の年を迎え、5年に1度のNPT運用検討会議が開催されます。この会議において、意義ある成果を生み出すために、昨年11月にここ長崎で開催された核軍縮に関する「賢人会議」の提言等を十分踏まえながら、各国に積極的に働きかけていく決意です。
(N.8) 私たちには、唯一の戦争被爆国として、核兵器の非人道性を、世代や国境を越えて伝え続ける務めがあります。
(N.9) 被爆者の方々から伝えられた被爆体験を、しっかりと、若い世代へと語り継いでいく。
(N.10) そして、長崎や広島を訪れる世界中の人々が、被爆の悲惨な実相に触れることで、平和への決意を新たにすることができる。そうした取組を我が国として、着実に推し進めてまいります。
(N.11) 被爆者の方々に対して、保健、医療、福祉にわたる支援の必要性をしっかりと受け止め、被爆者の方々に寄り添いながら、今後とも、援護施策を総合的に推進してまいります。特に、原爆症の認定について、引き続き、一日も早く結果をお知らせできるよう、できる限り迅速な審査を行ってまいります。
(N.12) 結びに、市民の皆様のたゆみない御努力により、「国際文化都市」として見事に発展を遂げられた、ここ長崎市において、「核兵器のない世界」と恒久平和の実現に向けて力を尽くすことをお誓い申し上げます。
(N.13) 原子爆弾の犠牲となられた方々のご冥福と、ご遺族、被爆者の皆様、並びに、参列者、長崎市民の皆様のご平安を祈念いたしまして、私の挨拶といたします。』
13段落だ。長崎で行われた挨拶なので、段落番号にNを付した。これを、同年の広島での式典挨拶と比較してみよう。
まず、(N.1)。これは広島の(1.2)。「・・・式典に当たり」までの前文以外は全く同じ。
『(N.1) 本日、被爆74周年の長崎原爆犠牲者慰霊平和祈念式典に当たり、原子爆弾の犠牲となられた数多くの方々の御霊(みたま)に対し、謹んで、哀悼の誠を捧(ささ)げます。』
『(1.2) 原子爆弾の犠牲となられた数多くの方々の御霊(みたま)に対し、謹んで、哀悼の誠を捧(ささ)げます。』
(N.2)は(1.3)と全く同じ。
(N.3)は(1.1)と、犠牲者の数を変え、文の順序を変えただけ。
『(N.3) 今から74年前の今日、一発の原子爆弾により、一瞬にして街は焦土と化し、7万ともいわれる貴い命が失われました。人々の夢や明るい未来が容赦なく奪われ、一命をとりとめた方々にも、筆舌に尽くし難い苦難の日々をもたらしました。』
『(1.1) 今から74年前の今日、原子爆弾により、十数万ともいわれる貴い命が失われました。街は焦土と化し、人々の夢や明るい未来が容赦なく奪われました。一命をとりとめた方々にも、筆舌に尽くし難い苦難の日々をもたらしました。』
なるほど、第3段落まで、段落の順序を違えたのね。
146文字ある割と長い(N.4)は(1.4)と寸分違わず同じ。
48文字の(N.5)も(1.5)と寸分違わず同じ。
114文字の(N.6)も(1.6)と寸分違わず同じ。
(N.7)は、賢人会議の行われた場所にちなんだ変更のみ。広島では「一昨年、ここ広島から始まった」とし、長崎では「昨年11月にここ長崎で開催された」としたのみ。まぁ、挨拶の場所を考慮したか。
『(N.7) 明年は、核兵器不拡散条約(NPT)発効50周年という節目の年を迎え、5年に1度のNPT運用検討会議が開催されます。この会議において、意義ある成果を生み出すために、昨年11月にここ長崎で開催された核軍縮に関する「賢人会議」の提言等を十分踏まえながら、各国に積極的に働きかけていく決意です。』
『(1.7) 明年は、核兵器不拡散条約(NPT)発効50周年という節目の年を迎え、5年に1度のNPT運用検討会議が開催されます。この会議において、意義ある成果を生み出すために、一昨年、ここ広島から始まった核軍縮に関する「賢人会議」の提言等を十分踏まえながら、各国に積極的に働きかけていく決意です。』
50文字の(N.8)は(1.8)と寸分違わず同じ。
39文字の(N.9)も(1.9)と寸分違わず同じ。
(N.10)は(1.10)と同じだが、長崎では「長崎や広島」、広島では「広島や長崎」と順番を入れ替えて配慮している。
『(N.10) そして、長崎や広島を訪れる世界中の人々が、被爆の悲惨な実相に触れることで、平和への決意を新たにすることができる。そうした取組を我が国として、着実に推し進めてまいります。』
『(1.10) そして、広島や長崎を訪れる世界中の人々が、被爆の悲惨な実相に触れることで、平和への決意を新たにすることができる。そうした取組を我が国として、着実に推し進めてまいります。』
(N.11)は(1.11)と同じ。「今後も」が「今後とも」になったり、少し順番が変わっているが、内容を伴わない文章であることも含めて同じだろう。
『(N.11) 被爆者の方々に対して、保健、医療、福祉にわたる支援の必要性をしっかりと受け止め、被爆者の方々に寄り添いながら、今後とも、援護施策を総合的に推進してまいります。特に、原爆症の認定について、引き続き、一日も早く結果をお知らせできるよう、できる限り迅速な審査を行ってまいります。』
『(1.11) 被爆者の方々に対して、保健、医療、福祉にわたる支援の必要性をしっかりと受け止め、今後も、被爆者の方々に寄り添った援護施策を総合的に推進してまいります。特に、原爆症の認定について、引き続き、一日も早く結果をお知らせできるよう、できる限り迅速な審査を行ってまいります。』
(N.12)と(N.13)の結びの言葉は、広島では(1.12)の1段落に纏められている。しかしながら、内容はほぼ同じだ。場所の相違のみ変更している
『(N.12) 結びに、市民の皆様のたゆみない御努力により、「国際文化都市」として見事に発展を遂げられた、ここ長崎市において、「核兵器のない世界」と恒久平和の実現に向けて力を尽くすことをお誓い申し上げます。
(N.13) 原子爆弾の犠牲となられた方々のご冥福と、ご遺族、被爆者の皆様、並びに、参列者、長崎市民の皆様のご平安を祈念いたしまして、私の挨拶といたします。』
『(1.12) 結びに、「国際平和文化都市」として発展を遂げた、ここ広島市において、「核兵器のない世界」と恒久平和の実現に向けて力を尽くすことをお誓い申し上げます。原子爆弾の犠牲となられた方々のご冥福と、ご遺族、被爆者の皆様、並びに、参列者、広島市民の皆様のご平安を祈念いたしまして、私の挨拶といたします。』
いや~ぁ、或る意味すごく論理一貫している。挨拶の構成から内容まで、被爆地の地名を入れ替え、それぞれの被災者数に直した以外、見事に同じだ。
広島と長崎を変えただけ。
この言葉を届けたい相手は誰なのだろうか。誰にも届いてほしくないのだろうか。分析しきれない。
100.恒星になれなかった木星
概論の授業の最終回は、ミクロの物理学、量子科学に触れて、基礎方程式であるシュレーディンガー方程式を見せて、トンネル効果なんか説明して、無からの宇宙生成の可能性まで話して締めていたのだが、昨年やったら、難しすぎてわからないと、評判が大層悪かった。
そこで、今年は、直前、ギリギリになってから話題を変えて、不確定性関係だけに絞ることにした。それだけでは物足りないので、不確定性関係を使って水素原子の大きさを見積もり、ついでに、恒星になれない星の話を紛れ込ませるという三題話でいくことにした。最終回の前の回は、核融合で太陽が燃えており、その寿命を見積もるという話をしたので、まぁ、対(つい)になっていて良いかな、という程度で選んだ題材だ。
急遽話題を変えたので、シラバスには書いていない。契約書じゃないんだから、契約不履行とはならないだろう。
まずは、電子などの素粒子を想定して、その位置を測定することを考える。観測するためには、何か働きかけに対する応答をみなければならない。簡単には、光を当てて位置を測定すればよい。しかしながら、電子はミクロな対象なので、光を当てても光(電磁波)の波長より小さい距離は区別がつかない。どの点から散乱された光を観測しているのかわからないからである。顕微鏡では“分解能”として知られていることだ。したがって、位置測定の精度は、当てる光の波長λ程度であることがわかる。そこで、位置測定での不確定さをΔxと書くことにすると、
Δx ≒ λ
というわけだ。Δx より小さい距離は区別がつかないということ。こうして、精度良い位置測定のためには、あてる光の波長 λ を短くすれば良いと言える。

しかし、照射する光は運動量 p を持つ。第25回に記してあることだ。光(光子)の持つ運動量 p は
p = h / λ
だった。ここで、h はプランク定数で、h = 6.6×10-34 Js。でも、これを 2π で割ったℏ(エッチバー)= h / (2π) = 1.0545718×10-34 Js が基礎定数で、よく使われる。なので、
p = h / λ = 2πℏ / λ
波長 λ の短い光を当てるということは、運動量 p の大きな光を当てるということに等しい。
光を照射された電子は、光から運動量を得て、自分自身の運動量を変えてしまう。光を感知する観測装置はある程度の大きさを持っているので、光はある程度の開口角をもって観測されるはずである。なので、位置測定に関与する光がどの角度で入ってきたかは精確にはわからなくなるので、電子は光からどれだけの運動量を受け取ったかは、その範囲で分からなくなる。
こうして、光の照射による電子の運動量測定では、運動量測定の不確定さ Δp として
Δp ≒ 2πℏ / λ
の不定性が避けられないというわけだ。
位置測定と運動量測定を行うと、ともに不確定さが存在し、片方を小さくする、たとえば Δx → 0 とする為には λ → 0 とする必要があるが、このときには運動量の不確定は大きくなってしまう。だって、λ → 0 では運動量の不確定さ Δp の分母が零になって、Δp → ∞ になってしまうから。
不確定さの積は、
Δx Δp ≒ λ×(2πℏ/λ)≒ ℏ
となる。定数2π は無視した。こうして、ℏ(またはh)が 0 でない限り、左辺の積は零にはならない。この事実は不確定性原理と呼ばれ、上の関係式、Δx Δp ≒ ℏ を不確定関係と呼ぶ。
さて、この不確定性原理を用いて、水素原子の大きさを見積もっておこう。三題話の二題目。

水素原子核(陽子)は電子の 1860 倍の重さを持つので、水素原子核は動かないとして、その周りに電子がいるとしよう。水素原子のエネルギー E は
E = (1/2) me v2 - (e2/ 4πε0 r)
= p2 / 2 me -e2 / 4πε0 r
ここで、電子の質量を me = 9.1×10-31 [kg]、電子の速さを v、運動量は p = me v、位置エネルギーは陽子と電子の電気的エネルギーから -e2 / ( 4πε0 r) なっていることは認めよう。ここで、ε0 = 8.85×10-12 [A2 s4 /m3 kg] は真空の誘電率と呼ばれる量であり、また、e = 1.6×10-19 [C] は素電荷だ。電子は原子の中心から“原子の大きさ” r までのどこにいるか正確には解らない、つまり不確定なので、原子の大きさをrとして、r 程度の“位置の不確定さ”があると考えられる。すなわち
Δx ≒ r
よって、運動量の不確定さ Δp は、不確定性関係から
Δp ≒ ( 1 / Δx ) ×ℏ ≒ ℏ / r
と得られる。こうして、水素原子中の電子の運動量は不確定で、Δp 程度の運動量を持つと考えないといけないので、エネルギー E は
E ≒ (Δp)2 / 2 me - e2 / 4πε0
= ℏ2 /(2 me r2)- e2 / (4πε0 r) ・・・(1)
となる。これはある r で最小値を持つ。そこが安定な水素原子の大きさになる。

E が最小なので、E の接線の傾きが零になる点、つまり E の r による1 階微分が零になる点 r がエネルギー最小を与える。こうして、
dE/ dr=-ℏ2 /(me r3 ) + e2 / (4πε0 r2 )=0
よって
r = 4πε0 ℏ2 / me e2
= aB (=0.5×10-10 [m] ) ・・・(2)
が得られる。これが水素原子の“大きさ”と見積もれる。これは、ボーア半径とよばれ、改めて aB と書いた。
このとき、水素原子のエネルギー E は、(1)に(2)を代入して
E = ℏ2 / (2 me r2 )- e2 / (4 πε0 r)
= -me / (2 ℏ2 )×( e2 / (4πε0 ))2
= 13.6 eV
と得られる。これで、水素原子の大きさとエネルギーは決まった。
三題話の三題目。
木星は太陽のように核融合をおこして、自ら輝く星ではない。ということは、木星内部では構成原子の組成を変えないということだ。つまり、水素原子核は水素原子核のままで、重水素核やヘリウム原子核に核融合しない。核融合しない惑星の限界質量を大雑把に評価して見よう。
水素原子 N 個から星ができているとする。電子の質量は、水素原子核(陽子)に比べて軽いので、星の質量 M は、星内部の水素原子の個数を N [個]として、
M = N × mp ・・・(3)
として良かろう。ここで、mp は陽子、つまり水素原子核の質量だ。水素原子の大きさはボーア半径 aB をとり、
aB = 4πε0 ℏ2 / me e2 = 0.5×10-10 m
であった。
この星は、水素原子がぎっしり詰まっていて核融合するかしないかのギリギリにあるとすると、星の半径を R として
(4 / 3) πR3 =N×(4 / 3)πaB3
よって
R = N1/3 aB ・・・(4)
と見積もられる。核融合するほど重力は強くないので、重力エネルギー GM2 / R は電気エネルギー e2 / ( 4πε0 aB ) より小さいだろう。重力エネルギーが強ければ、水素原子核を押しつぶして核融合を始めるだろうから。ただし、原子は N 個あるので、電気エネルギーは水素原子すべて考えに入れて
G M2 / R < N×e2 / ( 4πε0 aB )
これを、星が核融合しない条件として設定して見よう。(3)から M を、(4)から R を消去して
G N2 mp2 / ( N1/3 aB ) < N×e2 / ( 4πε0 aB )
こうして、
N < ( e2 / (4πε0)×1/(G mp2 ))3/2
= [(e2 / (4πε0 ℏ c)) / (G mp2 / (ℏ c))]3/2
が得られる。プランク定数(を2πで割ったもの)ℏ、光速 c を分母分子に入れた。ここで、物理定数に数値を入れよう。光速 = 3.0×108 [m/s]、万有引力定数 G = 6.67×10-11 [m3 /kg s2]、陽子の質量 mp = 1.67×10-27 [kg]。無次元量が現れるように ℏ と c を入れておいた。無次元になる量は
e2 / (4πε0 ℏ c ) = 1 / 137
G / (ℏ c)×mp2 = 0.6×10-38
をうまく使うと、核融合しないこの星の陽子(水素原子核)の個数には制限があり、それは
N < 1054 個
となることがわかった。従って、この星の質量、半径には、おおよそ
M = N×mp < 2×1027 kg ・・・(5)
R = N1/3 aB < 5×107 m
という制限があることがわかる。ここで陽子質量 mp = 1.67×10-27 kg、水素原子の大きさ aB = 0.5×10-10 m を用いた。
ちなみに太陽では、N ≒ 1057 個の水素原子核が存在している。
木星の観測値を見ておこう。
質量:M ≒ 1.9×1027 kg
半径:R ≒ 7×107 m
(5)と、桁は合っている。木星は実際に燃えていないので、木星は惑星としては結構ぎりぎりの質量と大きさを持っていると結論できよう。これ以上重いと恒星になって輝いていただろう。
地球から太陽系内に 2 つの恒星が見られるのも、結構魅力的だったかも。
99.黄金比
息子も高校生となり、数学の先生から授業以外の数学の話を聴く機会が増えた様だ。先生が黄金比の話をしたようで、詳しくなっていた。教科書以外の知識が学問への導入になることは多い。
そういえば、自分自身も、正五角形の黄金分割の話を何かで読み、興味を持っていたことを思い出す。

図のように正五角形を書こう。三角形ABC と ACD と ADE の 3 つから 5 角形が作られるので、正五角形の内角の和は、180 度 × 3 = 540 度となり、正五角形の内角一つは540 ÷ 5=108 度だとわかる。三角形ABE を考えると、これは二等辺三角形で、しかも角BAE が 108 度なので、角ABE と角AEB はともに 36 度になる。正五角形の 2 頂点を結ぶ線分は BE だけでなく、AC も同じだ。だから、同じく、角BAC(=角BAF )も、角ABE(=角ABF )と同じく 36 度だから、三角形FAB は二等辺辺三角形になる。底角FBA と FAB が等しいから。こうして、三角形ABE と三角形FAB は相似だ。だから、それぞれの三角形の辺の長さの比として
AB : BE = BF:AB つまり AB / BE = BF / AB
だから、
(AB)2 = BE × BF ・・・(1)
となる。
また、角EAF は、角EAF =角BAE -角BAF = 108 度-36 度 = 72 度となり、角AEF = 3 6度だったので、三角形EAF を考えると、角EFA=180度 - 角AEF - 角EAF =180度-36度-72度=72度なので、三角形EAF も二等辺三角形であることがわかる。こうして辺の長さは AE = EF である。
今、正五角形の辺の長さを 1 としておくと、
AB = AE = EF = 1
である。さらに、対角線の長さ BE に対して、BE = x とすると、EF =1よ り、BF=x-1 になる。こうして(1)式から
12 =x ( x-1)
という式が得られる。整理すると、
x2 - x -1 = 0 ・・・(2)
となる。こうして、この2次方程式を解くと、
x = ( 1 + √5 ) / 2 (>0)
が得られる。こうして、
BF :FE = x-1 : 1
= x2 - x : x
= 1 : x
が得られる。1 行目から 2 行目は、比の値にそれぞれ x を掛け、2 行目から 3 行目へは(2)式から x2-x = 1 であることを使った。こうして正五角形の対角線は、他の対角線で、1:x に分割されることが分かった。この分割を、黄金分割と呼び、比
x = ( 1 + √5 ) / 2 =φ
を黄金比と呼ぶ。あらたに、φ という文字で定義した。φ はもちろん(2)式の正の解。√5 なんて無理数が入っているので、大体の数値を見ておくと
φ = 1.618033989・・・
さて、黄金比 φ が得られたが、下の図のように、辺の長さが φ と φ2 になる長方形ABCDを考えておこう。φ で割っておくと、変の長さの比は、
1 : φ
だ。φ は(2)式を満たすので
φ+1= φ2 ・・・(3)
だから、一辺の長さ φ の正方形AEFD をとると、長方形EBCF が残る。この長方形の辺の長さは図のように 1 と φ だ。1 になるのは(3)式から、φ2-φ=1 だから。
こうして、辺の長さが 1:φ(=φ:φ2 ) の長方形から正方形を取り除くと、また辺の長さが 1:φ の長方形が得られる。何度やっても同じだ。

そこで、下図のように次々正方形を取っていって、ついでに各正方形に 4 分の 1 の円を内接させていくと、アンモナイトの貝殻を横から見た様な図になる。生物は、進化の過程で、黄金比を知ることになったのだろうか。


さてさて、幾何学から離れてみよう。
黄金比 φ は、次のような式で表される(フォントが無いので見にくい・・・)。
φ = √(1+√(1+√(1+√(1+・・・
つまり、ルート(1+ルート(1+ルート(1+・・・)と、ルートの中に1+√・・・が繰り返し現れる。証明は簡単で、右辺を x とおくと、最初のルート(1+・・・)を考えると、・・・の部分はまたxそのものだから、
x = √(1 + x )
に他ならない。2 乗すると
x2 = 1 + x
となり、これは黄金比を求めた際の(2)式だから、解いて正の解を取ったら φ になる。
また、黄金比は連分数でも表される(フォントが無いのでちょっと書けないなぁ)。

右辺の1+の次の分数の分母も、1+となっていて、これは φ そのもの。そこで、φ の代わりにまた x と書くと、
x = 1 + 1 / x
となるので、x を掛けると
x2 = x + 1
となって、やっぱり(2)式だ。だから、解は黄金比 φ に一致する。
さてさてさて、黄金比 φ の逆数を見ておこう。
1 /φ = 2 / (1 + √5 ) = 2×( 1-√5)/ ( ( 1 + √5)×( 1-√5 ) )
= -( 1 -√5 ) / 2
= ( 1 + √5 ) / 2 - 1
= φ- 1
となる。計算するまでもなく(3)式を両辺 φ で割ると得られる式だ。何が言いたかったかと言うと、黄金比の逆数 1 /φ は黄金比の小数点以下の部分、0. 618033989・・・を表しているということ。φ から、整数部分の 1 を引いているから。
フィボナッチ数との関係も見ておこう。
一つがいの兎がいた。1 年目は成長するだけで何も起きないので、1 年後、つまり 2年目も兎は一つがいだ。2 年目中に一つがいの兎を産む。こうして、3 年目(の初め)には 2 つがいの兎がいる。4 年目にも一つがいの兎を産むが、昨年生まれたつがいの兎はまだ子を産まないので、4 年目には全部で 3 つがいの兎だ。5 年目には最初に生まれた兎が成長して一つがいの兎を産む。もとからいた一つがいの兎も一つがいの兎を産むので、5 年目には全部で 5 つがいだ。こうして数列を書いていくと、
1、1、2、3、5、8、13、21、34、55、89、・・・ ・・・(4)
となる。この数列は
Fn+2 = Fn+1 + Fn , (n=1, 2, 3, ・・・) ・・・(5)
と表される。これを提案者の名前を取って、フィボナッチ数、フィボナッチ数列と呼ぶ。たとえば、フィボナッチ数の 5 番目は(4)の 5 番目、5 だ。6 番目は 8 だから、(5)式に当てはめ、
F7 = F6 + F5 = 8 + 5 = 13
と、正しく(4)の並びの 7 番目の数が出ている。
このフィボナッチ数列で、一つ前の数字との比を取ってみる。例えば、
F4 / F3= 3 / 2 = 1.5
F5 / F4 = 5 / 3 = 1.6666666666・・・
F6 / F5 = 8 / 5 = 1.6
F7 / F6 = 13 / 8 = 1.625
F8 / F7 = 21 / 13 = 1.615384615・・・
F9 / F8 = 34 / 21 = 1.619047619・・・
F10 / F9 = 55 / 34 = 1.617647059・・・
F11 / F10= 89 / 55 = 1.611818181・・・
と、なんとなく、黄金比、1.618033989・・・に近づいてくるようだ。調子にのって、もっと計算すると
F20 / F19 = 6765 / 4181 = 1.618033963・・・
うん、近い。もうちょっと。
F50 / F49 = 12586269025 / 7778742049 = 1.618033989・・・
いい感じだ。
今、r n という形の数列が、フィボナッチ数列を決める(5)式を満たすとしてみよう。すると、
rn+2 = rn+1 + rn ・・・(6)
が成り立つはずだ。rn で割っておくと
r2 = r + 1 ・・・(6)’
となり、これは黄金比を求めた(2)式と同じだ。そこで、黄金比となる解を φ、もう一方を ψ としておこう。つまり、
φ=( 1 + √5 ) / 2 、 ψ=( 1 - √5 ) / 2
これはどちらも(6)式を満たすので、
φn+2 = φn+1 + φn 、 ψn+2 = ψn+1 + ψn
が成り立っている。だから、c、d を定数として、
c φn + d ψn
も(6)すなわち(5)式を満たしている。フィボナッチ数列の最初の 2 項はともに1なので、この条件から c と d を決めよう。n=1、n=2で
c φ + d ψ = 1 、 c φ2 + d ψ2 = 1
ここで、φ2 = φ + 1、ψ2 = ψ+ 1が成り立っているので、2 乗の項を消去すると、上の 2式から
c + d = 0
が得られる。よって、
( 1 = ) F1 = c φ + dψ = cφ- cψ= c√5 、よって、c = 1 / √5
と決まる。さらに
ψ= ( 1 - √5 ) / 2 = -1 / φ
の関係に気づけば、フィボナッチ数は黄金比を用いて、
Fn = ( φn -(-1 / φ)n ) / √5
と書けてしまう。n を十分大きくとると、( 1 / φ ) n → 0 となるので、Fn ≒ φn / √5になる。こうして、
Fn+1 / Fn -(n大きいとき)→ φ
が得られる。これが、隣り合うフィボナッチ数の比が、だんだん黄金比に近づいてくる理由だ。
黄金比の話からフィボナッチ数列まで来てしまった。最後に、95 回で見た「パスカルの三角形」にもフィボナッチ数列が現れることを見ておしまいにしておこう。図の矢印の並びの数を足すとフィボナッチ数列が現れる。

フィボナッチはイタリアのピサで生まれた。「ピサのレオナルド」が名前の様だが、「ボナッチオ ( Bonacci o) の息子」、filius Bonacci と呼ばれていたようだ。filius が息子。フランス語では fils だ。filius はラテン語そのまま、イタリア語になっている。
イタリアのフィレンツェで国際会議が行われたときに参加したが、学会の合間にエクスカージョン(遠足)があり、ピサに行った。ピサの斜塔に上がり、ガリレオが振り子の等時性を発見した教会に行き、と定番コースの観光をしている最中に、数学の研究所を見つけた。Laboratorio FIBONACCI という名の研究所であった。

98.ブランコ
ブランコ、児童公園なんかに備えられているあれだ。
ブランコの存在は、古くは紀元前2000年より以前に遡るらしい。メソポタミア文明、今のシリアあたりのシュメールだ。もとはどうやら、宗教儀礼、特に豊穣祈願で使われていたらしい。葡萄が生産される地方では、ブランコを漕ぐことは葡萄の豊作を祈願した宗教儀式だったそうだ。葡萄の房が揺れるのと、ブランコが揺れるのと、連想したのかもしれない。
ロシアでは亜麻の豊作を、タイでは稲の豊作を祈願するため、ブランコを漕いでいたそうで、世界中に広まっている。高く漕ぐほど農作物は良く成長すると考えれていた。
中国ではブランコのことを鞦韆(しゅうせん)と呼ぶ。冬至の頃にブランコを漕いで、太陽の復活を願ったようだ。
朝鮮半島にも伝わる。春、旧暦5月、田植えの頃、田植えは主に女性が行っていた。そのとき、女性はブランコを漕ぐ。やはり豊作祈願だ。と同時に、働く女性の邪気払いのため、菖蒲を飾った端午の節句を行っていたようだ。だから、もともと端午の節句は、男の子のためのものではなくて、女性のためのものだった。
奈良時代くらいには日本に入ってきて、鎌倉時代には武士が抜鈎する世の中になったので、菖蒲の読みから「尚武」が連想され、男の子の節句になって、現在まで続いている。でも、ブランコを5月の端午の節句に漕ぐ朝鮮半島の影響か、俳句の世界では、鞦韆は春の季語に分類されている。
ブランコの語源は諸説あるようだが、おそらく、ポルトガル語のバランソ、balançoだろう。ポルトガル語でブランコのこともさすが、英語で言うところのバランスでもある。また、ポルトガル語-英語辞書を見ると、swing とも書いてあるので、まさにブランコが揺れることに応じている。
ところで。
授業で振動での共鳴現象の話をする。強制振動の運動方程式を解いてみせるのだが、現象としてはブランコを漕いでいるときに後ろから押して貰う場合が挙げられる。
しかし、人に押して貰う手伝いなしにブランコは漕げる。良く学生さんが勘違いするので、ブランコを一人で漕げるのはパラメータ共鳴という現象であることを説明するが、数式を使うと時間がかかるので、たいがい省略する。
微分の計算をしないといけないので厄介だが、一応ここに残しておこう。
振動の運動方程式は、振動する物体の座標をq(t) として
d2 q(t) / dt2 + ω2 q(t) = 0 ・・・(1)
となる。微分を知らない方は読み飛ばして貰おう。tは時間変数。この微分方程式の解は
q(t) = A sin ωt + B cos ωt
となる。AとBは積分定数。三角関数のかたちで振動する解だ。振り子の場合、ωと書いた“角振動数”は、振り子の紐の長さをl、重力加速度をgとして
ω=√(g / l )
となっている。振り子の時はq(t) は、鉛直方向とブランコの紐(鎖?)の為す角度となる。
今度はωが時間tに依存している場合を考える。振り子の場合、ひもの長さlが周期的に時間変化するとしよう。l0 を基準の紐の長さとして、その周りに周期的に伸び縮みするとしておこう。
l = l(t) = l0 ( 1-h cos γt )
h は1に比べて小さいとして、( 1-x )-1 ≒ 1 + x +・・・という展開式を用いると
ω(t)2 = g / l(t) ≒ g / l0 ×( 1 - h cos γt ) -1 = ω02 ( 1 + h cos γt )
となる。ここで、定数として、ω0 = √(g / l0 ) を定義した。運動方程式(1)は
d2 q(t) / dt2 + ω02 ( 1 + h cos γt ) q(t) = 0 ・・・(2)
と書き直せる。これを近似的にでも解くのは大変なので授業では省略してしまう。詳しい分析では、ひもの基準の長さl0 を周期的に変化させるときの角振動数γが、基準の振り子の角振動数ω0 と
γ= 2ω0 / n (nは自然数)
の関係にあるときに共鳴現象が起きることが知られている。n = 1 の時に特に大きな共鳴が得られるので、ここではその場合に限ろう。こうして
γ= 2ω0 + ε
とおいてみる。εは小さな量とする。だって、ブランコを漕ぐときに、そんなにうまく自分でコントロールする角振動数γを、ブランコの固有の角振動数ω0 にあわせられないんだから、ずれを入れておいて、でもまぁ、ずれは小さいとしておこうというわけだ。
こうして、運動方程式はさらに書き直せて
d2 q(t) / dt2 + ω02 ( 1 + h cos [ ( 2ω0 + ε)t ] ) q(t) = 0 ・・・(3)
になる。
解q(t) を
q(t) = a(t) cos[ (ω0 +ε/ 2 ) t ] + b(t) sin[ (ω0 +ε/ 2 ) t ] ・・・(4)
とおいて、運動方程式(3)に代入してみよう。ここで、aとbの時間微分、da(t) / dt 、db(t) / dt が小さな量εと同じ程度の量だとする。そして、aとbの時間についての2階微分、d2a(t) / dt2 、d2b(t) / dt2 はεの2乗ほど小さいとして無視する。さらに、運動方程式に代入した場合、cos[ 3(ω0 +ε/ 2 ) t ] や sin[3 (ω0 +ε/ 2 ) t ] の項が出てくるのだが、これらは小さい量hの2乗程度になることがわかっていて、これらも無視しよう。この項まで考慮するには最初に仮定した解q(t)にもcos[ 3(ω0 +ε/ 2 ) t ] や sin[3 (ω0 +ε/ 2 ) t ] の項を入れておく必要がある。ここではεもhも1次の項まで考慮する近似を取っているとして、出てきたcos[ 3(ω0 +ε/ 2 ) t ] や sin[3 (ω0 +ε/ 2 ) t ] の項を無視してしまう近似を使う。そうすると、途中の計算は全部端折って、(4)を(3)に代入した方程式から近似的に
-ω0 ( 2 da(t) / dt +b(t)ε+ ω0 h b(t) / 2 ) sin[ (ω0 + ε/ 2 ) t ]
+ω0 ( 2 db(t) / dt -a(t)ε+ ω0 h a(t) / 2 ) cos[ (ω0 + ε/ 2 ) t ] ≒ 0
という式が得られる。すべての時間tでこの式が成り立つためには
2 da(t) / dt +b(t)ε+ ω0 h b(t) / 2 = 0
2 db(t) / dt -a(t)ε+ ω0 h a(t) / 2 = 0
の2式が成り立っていればよい。さらに、a0 、b0 を時間に依存しない定数としてa(t)、b(t)を、
a(t) = a0 est 、b(t) = b0 est
とおいて、上の2式に代入してからest で割っておくと、ついでに2でも割っておくと
s a + bε/ 2 +ω0 h b / 4 = 0
s b - aε/ 2 +ω0 h a / 4 = 0
が得られる。最近の高校生は数学で行列を習わないと聞くが、行列とベクトルで上の2式を一発で表すと(といっても、ここでは書けないのだが・・・)
Γ s ( ε +ω0 h / 2 ) / 2 〕 |a|= |0|
L -( ε-ω0 h / 2 ) / 2 s 」 |b|= |0|
みたいに書ける(苦しい)。
a = 0、b = 0以外の解を持つには、行列の行列式が0であれば良いので、行列式を0とすると
s2 + ( ε2 -ω02 h2 / 4 ) / 4 = 0
が得られる。こうして、
s =( 1 / 2 )× √( (ω0 h / 2 )2 -ε2 ) ・・・(5)
が出てくる。結局、近似的ではあるが、q(t) が求まり、
q(t) = a0 est cos[ (ω0 +ε/ 2 ) t ] + b0 est sin[ (ω0 +ε/ 2 ) t ]
が得られる。sが純虚数、つまり(5)式で、
(ω0 h / 2 )2 -ε2 < 0
のときはei|s|t = cos (|s|t) +i sin (|s|t) だから、やっぱり振動する解になるので、共鳴は起きない。ところが
(ω0 h / 2 )2 -ε2 > 0 ・・・(6)
のときにはsは実数なので、解q(t) は時間tが経つと、est でどんどん大きくなる。ブランコだったら、振れる角度q(t)が時間とともにどんどん大きくなるということなので、漕げているというわけだ。
ブランコを漕いでどんどんブランコの振れ幅が大きくなるためには、(6)の条件から、角振動数の2ω0からのずれεが
-hω0 / 2 < ε< hω0 / 2
の範囲に収まっていれば共鳴が起きてブランコが漕げるというわけだ。
では、ブランコで“ひも”の長さをどう変化させれば良いのか?
ここで言う“振り子の紐の長さ”は、支点から重心までの長さと思えばよいので、ブランコを漕ぐときであれば紐の支点から重心の高さまでが“振り子の紐の長さ”とみなせる。重心の高さを変えるために、ブランコを立ち漕ぐするときであれば、体を伸ばしたり縮めたりするわけだ。ブランコが行って帰ってくるまでの周期Tは角振動数ω0に反比例、すなわちT = 2π/ ω0 だ。だから、ブランコが一周期する間に、体の上下動を2回することになる。だって、体の上下の一周期は2π/ γ= 2π / 2ω0 = T / 2だから、ブランコの一周期の半分で上下動を1回すれば“パラメータ共鳴”してブランコが漕げるというわけだ。ブランコの一周期であれば体の上下動は2回。こうして、ブランコが最高点に達した時に体を伸ばし、最低点を通過するときに体をかがめて縮め、次の最高点でまた体を伸ばす。この繰り返しでブランコは漕げる。
座ってブランコを漕ぐときには、最高点ではて膝から下の足を曲げて胴体と垂直方向に伸ばして重心を上げ、最低点では足を普通にぶらんと下の方に垂らして重心を下げ、次の最高点ではまた胴体と垂直方向に伸ばして重心を上げて、ブランコの半周期で1回の重心の上下動を行う。
おそらく立漕ぎでの重心の移動のほうが、座って漕ぐ場合の重心の上下移動より大きいだろう。だから、立漕ぎした方が、若干hが座り漕ぎの時より大きい。εが同じだと、hが大きい方がsが大きくなるので、est の割合で増大する振幅は、同じ時間tだけ漕いでいても立漕ぎの方が大きくなるというわけだ。
97.ライプニッツの積分法
ニュートンとは独立に、微積分法はライプニッツによっても発見されている。ニュートンによる積分法を説明したのに、ライプニッツに触れないのは片手落ちの様な気がするので、ライプニッツによる求積(積分)法を記しておこう。
ライプニッツは、ある曲線の下の( x 軸と囲まれた)面積を、“等しい長さ(横幅)の縦座標の総和”とみなした。これが積分だ。逆に、“縦座標と横座標それぞれの値の差が小さくなっていくときに、それらの比によって、曲線の接線が決まる”ことに気づいた。これが微分だ。
1675 年のノートによって、積分を見ておこう。

図で、曲線の下の OAB の面積は、縦座標 y の総和と見なした。“すべて”というラテン語の形容詞、omnis の属格、“すべての”に対応するomnium から、y の総和を
omn. y ( OAB の面積) ・・・(1)
と書いた。
一方、OBC は、面積 xw の長方形の総和だ。ここで、w は、横座標 x が幅 1 隣に進んだ時の y の増分だ。x+1 と x での y の差のこと。そこで、OBC の面積は、
omn.xw ( OBC の面積) ・・・(2)
と書ける。また、OA の長さを、ult.x と書き、OC の長さは w の総和、omn.w なので、長方形 OABC の面積は
ult.x , omn.w (長方形OABCの面積) ・・・(3)
と書く。ここで、コンマ( , )は、掛け算(×)の意味で使われている。こうして、(1)、(2)、(3)から、面積の関係として
ult.x , omn. w = omn.y + omn.xw
が得られる。ここで、右辺の y は、w の総和なので、
y = omn.w
と書けるので、これを代入すると
ult.x , omn.w = omn.omn.w + omn.xw
すなわち、
omn.xw = ult.x , omn.w -omn.omn.w ・・・(4)
と書き直される。
さて、まずは、
y = x
の曲線(直線)を考えよう。このときには、
y = omn.w = x
で、x が 1 単位進むと、y は 1 増えるので、w = 1 だ。したがって、(4)から、ult. x = xと書いて、
omn.x = x2 -omn.x
が得られる。整理すると
omn.x = x2 / 2
となる。要するに、y = x の曲線の下の面積は、x2 / 2 であるということで、y = x を x について積分したことになっている。
次いで、今度は、
w = x
としよう。(4)は
omn.x2 = x × omn.x - omn.omn.x
となるが、omn.x = x2 / 2 を先ほど求めたのでこれを代入すると
omn. x2 = x3 / 2 - omn.x2 / 2
となり、整理して、
omn.x2 = x3 / 3
が得られる。y = x2 の曲線の下の面積が x3 / 3 というわけで、y= x2 を x について積分したことになっている。
次は w = x2 といった具合にこの操作を繰り返していくことで、結局
omn.x n = xn+1 / (n+1)
が得られる。y= x n を x について積分したものは、 xn+1 / (n+1) となるということ。
ライプニッツが最初に使った記号、omn.は、ラテン語で総和を意味する summa omnium から来ている。omnium は先ほど記した、「すべての」の意味であり、summa は「和」のことだ。英語に入って、sum になる。ライプニッツは、最初用いていたomn. の代わりに、summa の頭文字の s を引き延ばして長くしたものを、新たに積分の記号にした。∫ だ。曲線 y ( = y(x) )の下の面積を、∫ y と書き、さらに後になって ∫ y dx と書くようになった。現在の記法だ。
微分は、“逆求積”であり、
∫ ℓ = ya としたときに ℓ を求める
演算とした。右辺は“面積”ということで、2つの変数の積でわざわざ書いている。ライプニッツは、積分も微分も“演算”としてとらえていて記法を生み出した。一方ニュートンは、積分は、x' = f (t) を x について解く“問題”と捉えていたようだ。
ちなみに、ライプニッツが最初に使ったラテン語の omnis であるが、「すべての」という属格が omnium であり、「すべてのために」という与格が、omnibus (オムニバス)だ。そこで、「すべての人のため」にあった乗合馬車のことが omnibus と呼ばれ、その後、馬車から自動車になり、やがて、omnibus が略されて bus になった。
通りを走っているバスって、ラテン語の変化する語尾じゃないか。
さらに、複数の独立した作品を一つに纏めた映画なんかを、オムニバス作品と呼ぶようになり、現在、大学で一つの講義を複数教員が行う授業形態を、オムニバスと呼んでいる。
オムニバス授業の準備をそろそろせねば・・・。
96.ニュートンの流率法
物理の授業をしていると、どうして微分や積分が物理に出てくるんだ、という文句が学生さんからよく出てくる。
でもね、力学の問題を解くために微分積分が生み出されたんだから仕方がない。
ライプニッツも同時期に微分積分学を考案していたものの、ニュートンは、力学の問題を扱うところから微分積分学を生み出した。力学は質点の運動の記述が大元にあるが、質点は運動しているので、もともと動的なものである。質点の運動の軌跡は、動点が辿る軌跡だ。平面曲線を考えると、平面はxとyの座標で表されるとすると、平面上の曲線は、ある関数 f(x,y)=0 で表される曲線に他ならない。例えば、半径 a の円は、f(x,y) =x 2 + y2 -a2 = 0 を満たす曲線だ。これを、点 (x,y) が“時間”とともに動いていった軌跡と考えるというわけだ。幾何学的に「原点からの距離 a が一定の点の集合」としてではなく、「動点が曲率一定(曲がり具合一定)で動いていった時の軌跡」を『円』と捉えるようなものだ。
動点が動いていく割合を、ニュートンは、「流率的速さ」あるいは単に「流率」と呼んでいた。そこで、ニュートン流の微分積分学は「流率法」と呼ばれる。
2次元平面で、“流量” x、 y の“流率”を、x'、y' と書くことにしよう。本当は x の上に黒丸・(ドット)を付けて書くのだが、フォントが無いので、代わりにダッシュを付けておこう。
こうして、各瞬間に描く無限に小さな線分の長さは速さに比例することから、O を“瞬間的時間”、x'、y' を x、y の流率(的速さ)として、ある瞬間に x、y であった長さは、次の瞬間には x + x'O、y + y'O になることが分かる。
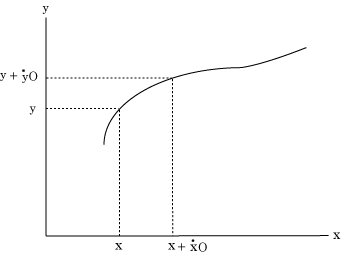
動点の曲線は f(x,y) = 0 で表されているので、
f(x,y) = 0
f(x+x'O, y+y'O) = 0
はともに曲線上にあるので、これらを連立させる。こうして、接線の傾きは、y 方向に動いた距離を、x 方向に動いた距離で割り算すれば得られるので、
y'O / x'O = y'/x'
として得られる。
具体的にやってみよう。
f(x,y) = x4 -ax2 -y
としてみる。f(x,y) = 0 の曲線とは、
y= x4 -ax2 ・・・(1)
のことだ。ここで、f(x+x'O, y+y'O) = 0でもあるので、代入して
f(x+x'O, y+y'O) = ( x+x'O)4 -a(x+x'O)2 -(y+y'O)
= 4x3 x'O-2axx'O-y'O+( O2 の項)+( O3 の項)+( O4 の項)
= 0 ・・・(2)
だ。ここで、(1)を使った。O は“瞬間的時間”であり小さいので、O2 、O3 、 O4 の項は小さいので無視しておき、(2)の両辺を O で割る。(2)の両辺を O で割ってから、残った O は小さいので無視すると言った方が良い。とりあえずやってみると、
4x3 x'-2axx'-y' = 0 、すなわち、y'/ x' = 4x3 -2ax
が得られる。この y' / x' が、点 (x,y) での曲線 f(x,y) = 0 の接線の傾きだ。これは今で言うところの、y を x で微分して得られる微係数を求めたことに他ならない。
では、微分の逆はどうだろうか。
1669 年にニュートンは、曲線の“下”の部分の面積、すなわち、曲線と x 軸に囲まれた面積を求める3つの規則を与えた。その内の「規則1」を見ておこう。規則1は
『もし、y = axm/n であれば、n / (m+n) × ax(m+n)/n が領域 ABC の面積に等しい』
というものだ。証明は「例から明らかである」と言って、ニュートンは6つの具体例を与えている。そのうちの一つが
「面積 S が、S = (2/3) × x3/2 となる曲線は?」
というものだ。ちょっと見ておこう。

図で、AB' の長さを x+O としておこう。AB の長さを x とするので、BB' の長さは Oだ。ただし、O は微小とする。今、長方形 BPQB' の面積が BCC'B' の面積と等しくなるように線分 PQ を引いたとする。BP の長さを v としよう。面積 S が S = (2/3) × x3/2 なので、両辺を 2 乗しておいて、
S2 = (4/9) x3 ・・・(2)
としておく。x が x から x+O に進んだ時の面積の増分は長方形 BPQB' の面積と等しいというのだから、BPQB' の面積は O×v より
(S + Ov )2 = (4/9) (x + O )3
が成り立っている。両辺展開しよう。
S2 +2SvO + v2O2 = (4/9) × (x3 +3x2O + 3xO2 +O3)
ここで、(2)から、S2 = (4/9) x3 であることを用いてから O で割ると
2Sv + v2O = (4/9) × (3x2 + 3xO +O2)
が得られる。ここでニュートンは
『もし BB' が無限に小さい、つまり O が零であると仮定すると、O がかかって
いる項は消え、かつ v は y に等しくなるので
2Sy = (4/9) 3x2 、すなわち y = x1/2
に還元される( S = (2/3) x3/2 を用いた)。』
として、問題を解いた。つまり、
『 y = x1/2 の曲線の下の面積( x 軸と囲む面積)は、S = (2/3) x3/2 である』
ここで、S = (2/3) x3/2 = 2 / (1+2) x(1+2)/2 であるので、ニュートンは
『S = n / (m+n) × ax(m+n)/n を取り上げ、面積 S を与える曲線は y = axm/n であ
ることを証明する予定である』
とした。この証明は簡単で、両辺 n 乗してから、上でやったことと同じことをすればできる。どうも、ニュートンは書き残していないようだが。
積分法の発見だ。1669 年、おそらく 1664 年から 1666 年の間に、ニュートンによる。
95.パスカルの三角形からニュートンへ
nを自然数として、( x + y )n の展開は比較的容易にできるが、逆の因数分解はなかなか難しい。
高校生になった息子が、
x4 + 4 y4 を因数分解せよ
という問題に出くわし、どうしたらよいかわからないようだった。
物理の研究を30年近くしている身にも、こんなに綺麗な数式を、なぜわざわざ因数分解するのか?という疑問を持つが、練習問題だから仕方がない。
結局息子は自分で解いたが、答えは
x4 + 4 y4 = ( x2 +2 x y + 2 y2 ) ( x2 -2 x y + 2 y2 )
左辺と右辺のどちらが美しいか?
でも、そんなこといったら、i = √(-1) という、2乗したらー1になる、つまり i 2
= -1 になる虚数単位を使えば
x4 + 4 y4 = ( x2 + i 2 y2 ) ( x2 - i 2 y2 )
= ( x + √2 i3/2 y ) ( x-√2 i 3/2 y ) ( x-√2 i 1/2 y ) ( x+√2 i 1/2 y )
= ( x + √2 ei(3/4)π y ) ( x-√2 ei(3/4)πy ) ( x-√2 ei(1/4)πy ) ( x+√2 ei(1/4)πy )
ともできるぞ?ここで、i 3/2 = ei(3/4)π =(-1 + i ) / √2、また、 i 3/2 = ei(1/4)π =(1 + i ) / √2
だ。
( 1 + x )n を展開した時の係数を、2項係数と呼ぶ。1665年、二項定理に現れる二項係数が、パスカルの三角形として簡単に表された。二項定理は
( 1 + x ) = 1 + x
( 1 + x )2 = 1 + 2 x + x2
( 1 + x )3 = 1 + 3 x + 3 x2 + x3
( 1 + x )4 = 1 + 4 x + 6 x2 +4 x3 + x4
・・・・
( 1 + x )n = nC0 + nC1 x + nC2 x2 + ・・・ + nCn xn
ただし nCr = n(n-1)×・・・×(n-r+1) / (1・2・3×・・・×r)
となる。ここで、xr の係数を並べると
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
・・・・・・・・・・・・
と三角形に並ぶが、中の数字は必ず、上斜め右と上斜め左の数の和になっている。例えば 5 段目の 6 は、右斜め上の 3 と左斜め上の 3 を足した数になっている。これをパスカルの三角形と言う。
少し並べ替えて、(1 + x )n の係数を縦に並べよう。一番上の段は、n の値。
|
n=0 |
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
1 |
3 |
6 |
10 |
|
|
|
|
1 |
4 |
10 |
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
1 |
そうすると、右へ右へ新たな数字を書き込むには、左斜め上と左の数字を足していけば良いことが見て取れる。たとえば、n = 5 の 3 段目の 10 は、左斜め上の 4 と左の 6 を足したものだ。空欄は 0 と思う。
ニュートンは、この表を、n が負の時に拡張した。一番上の段は、n の値。
|
-5 |
-4 |
-3 |
-2 |
-1 |
n=0 |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
← x0 |
|
-5 |
-4 |
-3 |
-2 |
-1 |
|
1 |
2 |
3 |
4 |
5 |
← x1 |
|
15 |
10 |
6 |
3 |
1 |
|
|
1 |
3 |
6 |
10 |
← x2 |
|
-35 |
-20 |
-10 |
-4 |
-1 |
|
|
|
1 |
4 |
10 |
← x3 |
|
70 |
35 |
15 |
5 |
1 |
|
|
|
|
1 |
5 |
← x4 |
|
-126 |
-56 |
-21 |
-6 |
-1 |
|
|
|
|
|
1 |
← x5 |
|
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
|
|
|
|
|
|
|
表は下へ、無限に続く。n が負の時の表の作り方は、右隣の数字から真上の数字を引くことで得られる。例えば、n = -3 の時の4段目、x3 の係数になる-10 は、右隣の-4 から真上の 6 を引く、つまり、-4-6 = -10 として得られる。こうして、n ≧ 0 のパスカルの三角形から、n が負の左側へ表を拡張していく。こうすると、例えば、n =-3をみていくと、確かに
( 1 + x )-3 = 1 - 3 x + 6 x2 - 10 x3 + 15 x4 -21 x5 +・・・
と、無限に続く二項展開が得られる。微分積分学を学んでテーラー展開を知っている人は、x = 0 の周りのテーラー展開をしてみるとよい。
1676 年には、ニュートンは、n が分数の場合の展開にも成功する。ただし、パスカルの三角形を直接拡張したものではないことを、1676 年の手紙で示している。( 1-x2 )n 、(n=0,1,2・・・) のグラフの下の面積を求める問題から、n = 1 / 2 の場合への補間を考えて得たそうだ。ニュートンが書いたように書くと(下付き棒線は本当は上に書いている、また分数は分数として書いている)
P +PQ |m/n
= P m/n + (m / n ) AQ + ( m-n ) / (2n) BQ + (m-2n) / (3n) CQ + (m-3n) / (4n) DQ +&c
ここで、P は第1項、Q は残りの項を P で割ったもの、A、B、C、D はすぐ前の項といったことだ。
具体例を見ておこう。( 1 + x ) 1/2 でやってみよう。1 + x の平方根だ。見比べると P = 1、Q = x、m = 1、n = 2 だ。A は前の項、Pm/n = 1 、B も前の項、(m/n)AQ =(1/2)×1×x、C も前の項、(m-n) / (2n) BQ = (1-2) / (2×2) ×(x/2) × xだ。こうして、
( 1 + x )1/2 = 1 + (1/2) x -(1/8) x2 + (1/16) x3 -(5/128)x4 +・・・
となることが確かめられる。これも、テーラー展開を知っていると確認できる。