５３．ホームランが打ちたい

　昭和時代を3分割していうならば、昭和後期が始まった頃のこと、スポーツ観戦と言えばテレビのプロ野球くらいしかなかった。地域性によるが、六甲おろしが流れていた。通っていた銭湯の下駄箱は、いつも田淵の背番号 22 だった。

　贔屓の球団は、自分が生まれてから一度も優勝していなかった。ところが、大学 2 年のとき、優勝してしまった。21 年振りの優勝であった。中西が最後に投げて優勝を決めた試合は長引き、友達の下宿で翌日のドイツ語の授業の予習会を 4 人で行う曜日だったのだが、さすがに遅れて参加した。祝勝のビールを買い込んで。「どうせ遅れてくると思った」と、広島出身や盛岡出身の友達には大目に見てもらえた。

　バース・掛布・岡田の最強打線の頃だった。それを過ぎると、一度優勝してしまったこともあり、急に興味がしぼんだ。それ以降、高校野球を含めても、あまり野球は見ない。

　ある日、研究室の外線電話が鳴った。どうせ、「東京で投資のマンション買いませんか」の類だろうと思って、極めて不機嫌なトーンで電話に出ると、子供が水泳の全国大会で東京辰巳の国際水泳競技場で泳いでいたが、そっち方向にある信頼のおける某所からの電話で、トーンを戻して話を聞いてみると、ホームランを打つ企画をしているのだが、ホームランを打てない子でも打つ方法は無いものか、しっかり練習して挑戦するのだが、どうしても打てなかった場合、ブログの 50 回にあった「スーパーボールの衝突」なんかを利用して、ホームランが打てない子でも打たせてあげられないものか、との内容の電話であった。スーパーボールは多段階の衝突を考えると、どんどん速さが早くなる（50 回参照）という話だったのだが、さて、それと同じ原理を野球のバットに仕込めるものか、ちょっとアイデアがなかった。とりあえず、野球の統一球は跳ね返り係数（反発係数）が決まっているので、反発係数の大きな素材で実験してみたら、程度の返答しかできず、その旨お話しして電話を措いた。

　言った手前、そのあと、野球のボールをバットで打ったらどうなるかを、反発係数を変えたらどれくらい飛距離が伸びるかを中心に考えてみた。図1 の大きい円がバットの断面、小さい円がボールの断面とする。図で左向きに速さ v [m/s] で飛んできたボールを、バットを右向きに速さ V [m/s] で振って当てる。バットとボールの接触点とバットの中心を結ぶ線が、図のように水平面と角度 θ を持って衝突したとしよう。水平方向をx 方向、鉛直上向き方向を y 方向と呼ぶ。

　　　  　　　

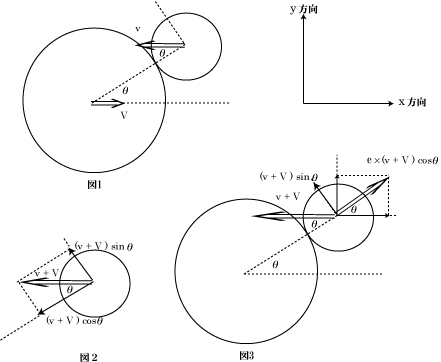
　図2 はバットの静止系でボールを見たものだ。バットに乗っかって考えると、ボールはバットに向かって速さ v + V で飛んでくるように見える。バットとの衝突面に垂直方向の速さの成分は、図の様に ( v + V ) cosθ となっている。一方、衝突面に沿った速さの成分は (v + V ) sinθ である：

　　　バットの静止系から見て、

　　　　　衝突直前の速さの衝突面に垂直な成分　　( v + V ) cosθ

　　　　　衝突直前の速さの衝突面に平行な成分　　( v + V ) sinθ

衝突面に垂直な方向の速さの成分は、衝突直後には、跳ね返り係数（反発係数）を e と書くと、e の割合で遅くなっている。もちろん 0 ≦ e ≦ 1だ。反発係数の定義は、衝突面に垂直な速度成分に対して

　　　　反発係数＝（衝突後の2物体の相対速度の大きさ）

　　　　　　　　　　　　　　　　　÷　　

　　　　　　　　　（衝突前の2物体の相対速度の大きさ）

と言える。だから、バットの静止系で見て、衝突直後の速さの衝突面に垂直な成分は、

e×( v + V )cosθ となる。衝突面に沿った、衝突面に平行な速度の成分は変わらない。

　　　バットの静止系から見て、

　　　　　衝突直後の速さの衝突面に垂直な成分　　e×( v + V ) cosθ　・・・（１）

　　　　　衝突直後の速さの衝突面に平行な成分　　( v + V ) sinθ　　 ・・・（２）

図3で、ボールから右斜め上方向に向かう2重矢印⇒が（１）、左斜め上を向いた矢印→が（２）だ。こうして、衝突直後にバットに対して持つボールの速さの水平方向の成分

v_x0^バットと、鉛直成分 v_y0^バット は、図3から

　　　　v_x0^バット= e ( v + V )cosθ×cosθ － ( v + V )sinθ×sinθ

　　　　v_y0^バット= e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ

と読み取れる。今度は、バットの静止系から私たちの居る本当の静止系に戻ろう。バットの静止系はバットとともに速さVで水平右向きに動いていたので、本当の静止系に戻すときには水平右向きの速度 V を加えればよい。私たちの静止系から見て、ボールはバットで打たれた直後、

　　　　v_x0= e ( v + V )cosθ×cosθ － ( v + V )sinθ×sinθ + V　　　・・・（３）

　　　　v_y0= e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ　　　　　　・・・（４）

という初速度でバットを離れるということだ。あとは、ニュートン方程式を解いて、飛距離を求めればよい。高等学校の物理の授業では「公式」を使って求める。大学に入って物理を専攻すると、1 回生ですぐに微分方程式としてのニュートン方程式を解いて求める。

　ニュートン方程式は

　　　　（質量）×（加速度）＝（力）

なので、ボールの質量を m [kg] 、水平方向の速度を v_x [m/s]、鉛直方向の速度をv_y [m/s]と書くと、水平の x 方向の運動方程式は

　　　m dv_x/dt = 0 　　　　・・・（５）

となる。ここで、dv_x/dt は v_x を時間 t で微分したもので、速度の時間変化が加速度なので、加速度の x 成分である。水平方向に力は働かないので、右辺は零だ。そうそう、空気抵抗は無視しておこう。

　鉛直方向には重力 mg が働く。ここで、g は重力加速度で、9.8 m/s²。下向きに力が働くので、負号に注意して、運動方程式は

　　　m dv_y/dt = －mg 　　　　・・・（６）

となる。（５）式は簡単で、v_x に時間変化が無いと言っているのだから、

　　　　v_x = （一定）＝ v_x0

だ。すなわち、水平方向には初速 v_x0 のまま、飛んでいく。ボールの位置 x の時間変化が水平方向のボールの速度 v_x になるので、位置 x は速さ(v_x) × 時間(t) なので、

　　　　x = v_x0 × t　　　　・・・（７）

でわかる。

　さて、鉛直方向の（６）式を解くと、

　　　　v_y = －gt + v_y0　・・・（８）

が得られる。実際に（８）を t で微分すると

　　　 dv_y/dt = －g 　　　　

が得られるが、これは（６）で両辺共通の m で割ったものに他ならない。また、（８）で時間 t = 0 の初期時刻では確かに初速 v_y0 になっている。鉛直方向のボールの位置 y を求めよう。位置 y の時間変化が速度 v_y であるので、

　　　　dy / dt = v_y

だから、右辺に（８）を代入して

　　　　dy / dt = －gt + v_y0　・・・（９）

これをyについて解くと（積分すると）

　　　　y = －g×t²  / 2 + v_y0×t　　・・・（１０）

が得られる。実際に t で微分したら（９）になることを確かめればよい。また、t = 0の、バットとボールが衝突した時間では、鉛直方向の高さを零とした。ボールの打点の位置を基準の高さ 0 と決めたということ。

　解いた答え（７）と（１０）から、ボールの飛距離がわかる。飛距離の位置を打点の高さ y = 0 としておこう。（１０）から y = 0 になる時間は、左辺の y に 0 を入れて

　　　　0 = (－gt / 2 + v_y0 ) t

とできるので、

　　　　t = 0  または　　t = 2×v_y0 / g

である。t = 0 は明らかに打った瞬間で、打点の高さは確かに 0 だが、飛距離を求めたいので、ボールが上がって落ちてくるまでの時間、t = 2×v_y0 / g を取る。この時間でボールは高く上がって落ちてくるが、その際、水平方向にはどれくらい飛んだかというと、（７）式だから

　　　　x = v_x0 × t = 2 v_x0 v_y0 / g

　　　　　= 2×[e ( v + V )cosθ×cosθ － ( v + V )sinθ×sinθ + V]

　　　　　　×[e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ]/ g

三角関数の公式を使ってちょっと整理しておくと

　x = [( v+V ) / g ] ×(1+e)×sin 2θ×[( v + V )×( e (cosθ)² －( sinθ)²  ) + V]　・・（１１）

が得られる。

　さぁ、数値を仮定して飛距離を見てみよう。もう一度確認だが、空気抵抗は無視している。プロ野球のボール、統一球というやつは、反発係数が 0.4034 から 0.4234 の間だそうだ。間を取って

　　　　e = 0.41

としておこう。ボールの速さは、時速 150 km とかだと、よう打たんので、時速 120 km  としてみる。それでも打ち返せないだろうなぁ。でもまぁ計算のため。

　　　　v_x0 = 120 km / 時 ≒　33.3 m/s

バットの長さは 106 cm 程度だそうだ。バットを持って体を回転させてバットのヘッドに速さVを持たせる。体の中心軸からバットを持つ手まで 40 cm 、バットの先から20 cm のところにボールが当たったとして、体の中心軸からおよそ r = 1.2 m のところにボールが当たったとする。バットを半回転、180 度回転するのに 0.2 秒でフルスイングしたとしよう。このとき、与えた角速度は ω=  π/0.2 rad/s。π は円周率で、角度をラジアンで測っている。そうしたら、バットの速さは

　　　　V = r×ω = 1.2×π/0.2 ≒　18.8 m / s ≒ 67.8 km / 時

時速 68 kmだ。重力加速度は g = 9.8 m/s² を使うので、（１１）式から飛距離 x [m] が、ボールがバットに当たった角度θの関数として求まる。数値計算の結果を描いてみよう。

　　　　　　　　

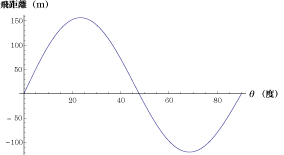
横軸が普通の単位、「度」で測った角度、縦軸が飛距離だ。角度 14 度で飛距離は 127 mとなり、角度 23.4 度のとき飛距離が最大で157 m になる。角度 33 度で再び飛距離は126 m 程度になる。フェンスの高さも考えないといけないが、14 度から 33 度でバットをボールに当てると、ホームランになりそうだ。角度 47 度を超えたあたりから飛距離がマイナスになるが、まぁ、キャッチャーのファウルフライというところだろうか。

　お題は、「ホームランが打ちたい」だった。普通にやっていては打てない（かもしれない）から、なんとか打とうという企画であった。とりあえず、反発係数の大きな場合を考えてみよう。スーパーボールを落下させて、床面に衝突したあと、最初の高さの 80 % 位まで戻ってきたという実験があるそうだ。高さ h [m] から落とすと、エネルギー保存則を使うと、床面に衝突する直前の速さは √(2gh) となることがわかり、この後  0.8 h の高さまで上昇するので、衝突直後の速さは √(2g×0.8h) となるので、反発係数は

　　　　√(2g×0.8h) / √(2gh) ≒ 0.89

で、およそ 0.9 だ。スーパーボールでホームランを狙おう。

　反発係数を 0.9 にして計算し直して見る。

　　　　　　　

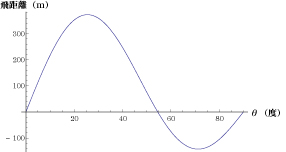
今度は、角度 6 度で飛距離は 136 m、角度 25.8 度で最大の飛距離 373 m がでる。角度47 度で 129 m まで落ちるが、120 m を超えているので、十分ホームランだ。当たる角度が少々悪くてもホームランが狙える。

　時速 120 km のボールを打つのは難しいし、フルスイングしてもバットの速度が速くならないかもしれない。空気抵抗もあるだろう。

　だけど、今までの条件で飛距離が最大 373 m 出るんだから、条件を緩めても、きっとホームランは打てる、よ。

　と、願っておこう。