96.ニュートンの流率法
物理の授業をしていると、どうして微分や積分が物理に出てくるんだ、という文句が学生さんからよく出てくる。
でもね、力学の問題を解くために微分積分が生み出されたんだから仕方がない。
ライプニッツも同時期に微分積分学を考案していたものの、ニュートンは、力学の問題を扱うところから微分積分学を生み出した。力学は質点の運動の記述が大元にあるが、質点は運動しているので、もともと動的なものである。質点の運動の軌跡は、動点が辿る軌跡だ。平面曲線を考えると、平面はxとyの座標で表されるとすると、平面上の曲線は、ある関数 f(x,y)=0 で表される曲線に他ならない。例えば、半径 a の円は、f(x,y) =x 2 + y2 -a2 = 0 を満たす曲線だ。これを、点 (x,y) が“時間”とともに動いていった軌跡と考えるというわけだ。幾何学的に「原点からの距離 a が一定の点の集合」としてではなく、「動点が曲率一定(曲がり具合一定)で動いていった時の軌跡」を『円』と捉えるようなものだ。
動点が動いていく割合を、ニュートンは、「流率的速さ」あるいは単に「流率」と呼んでいた。そこで、ニュートン流の微分積分学は「流率法」と呼ばれる。
2次元平面で、“流量” x、 y の“流率”を、x'、y' と書くことにしよう。本当は x の上に黒丸・(ドット)を付けて書くのだが、フォントが無いので、代わりにダッシュを付けておこう。
こうして、各瞬間に描く無限に小さな線分の長さは速さに比例することから、O を“瞬間的時間”、x'、y' を x、y の流率(的速さ)として、ある瞬間に x、y であった長さは、次の瞬間には x + x'O、y + y'O になることが分かる。
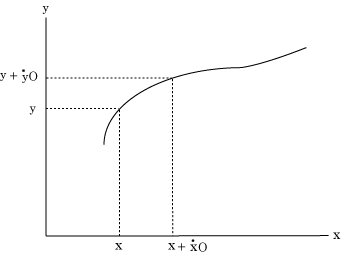
動点の曲線は f(x,y) = 0 で表されているので、
f(x,y) = 0
f(x+x'O, y+y'O) = 0
はともに曲線上にあるので、これらを連立させる。こうして、接線の傾きは、y 方向に動いた距離を、x 方向に動いた距離で割り算すれば得られるので、
y'O / x'O = y'/x'
として得られる。
具体的にやってみよう。
f(x,y) = x4 -ax2 -y
としてみる。f(x,y) = 0 の曲線とは、
y= x4 -ax2 ・・・(1)
のことだ。ここで、f(x+x'O, y+y'O) = 0でもあるので、代入して
f(x+x'O, y+y'O) = ( x+x'O)4 -a(x+x'O)2 -(y+y'O)
= 4x3 x'O-2axx'O-y'O+( O2 の項)+( O3 の項)+( O4 の項)
= 0 ・・・(2)
だ。ここで、(1)を使った。O は“瞬間的時間”であり小さいので、O2 、O3 、 O4 の項は小さいので無視しておき、(2)の両辺を O で割る。(2)の両辺を O で割ってから、残った O は小さいので無視すると言った方が良い。とりあえずやってみると、
4x3 x'-2axx'-y' = 0 、すなわち、y'/ x' = 4x3 -2ax
が得られる。この y' / x' が、点 (x,y) での曲線 f(x,y) = 0 の接線の傾きだ。これは今で言うところの、y を x で微分して得られる微係数を求めたことに他ならない。
では、微分の逆はどうだろうか。
1669 年にニュートンは、曲線の“下”の部分の面積、すなわち、曲線と x 軸に囲まれた面積を求める3つの規則を与えた。その内の「規則1」を見ておこう。規則1は
『もし、y = axm/n であれば、n / (m+n) × ax(m+n)/n が領域 ABC の面積に等しい』
というものだ。証明は「例から明らかである」と言って、ニュートンは6つの具体例を与えている。そのうちの一つが
「面積 S が、S = (2/3) × x3/2 となる曲線は?」
というものだ。ちょっと見ておこう。

図で、AB' の長さを x+O としておこう。AB の長さを x とするので、BB' の長さは Oだ。ただし、O は微小とする。今、長方形 BPQB' の面積が BCC'B' の面積と等しくなるように線分 PQ を引いたとする。BP の長さを v としよう。面積 S が S = (2/3) × x3/2 なので、両辺を 2 乗しておいて、
S2 = (4/9) x3 ・・・(2)
としておく。x が x から x+O に進んだ時の面積の増分は長方形 BPQB' の面積と等しいというのだから、BPQB' の面積は O×v より
(S + Ov )2 = (4/9) (x + O )3
が成り立っている。両辺展開しよう。
S2 +2SvO + v2O2 = (4/9) × (x3 +3x2O + 3xO2 +O3)
ここで、(2)から、S2 = (4/9) x3 であることを用いてから O で割ると
2Sv + v2O = (4/9) × (3x2 + 3xO +O2)
が得られる。ここでニュートンは
『もし BB' が無限に小さい、つまり O が零であると仮定すると、O がかかって
いる項は消え、かつ v は y に等しくなるので
2Sy = (4/9) 3x2 、すなわち y = x1/2
に還元される( S = (2/3) x3/2 を用いた)。』
として、問題を解いた。つまり、
『 y = x1/2 の曲線の下の面積( x 軸と囲む面積)は、S = (2/3) x3/2 である』
ここで、S = (2/3) x3/2 = 2 / (1+2) x(1+2)/2 であるので、ニュートンは
『S = n / (m+n) × ax(m+n)/n を取り上げ、面積 S を与える曲線は y = axm/n であ
ることを証明する予定である』
とした。この証明は簡単で、両辺 n 乗してから、上でやったことと同じことをすればできる。どうも、ニュートンは書き残していないようだが。
積分法の発見だ。1669 年、おそらく 1664 年から 1666 年の間に、ニュートンによる。