56.手で掛け算、続報
第 21 回で、1 から 5 までの数同士の掛け算を知っていたら、6 から 9 までの数同士の掛け算は両手の指を使ってできることを記した。最近、同じようにして、10 から 15までの数同士の掛け算を手で使ってできることを知った。ただし、ある数の 10 倍というのは知っていないといけない。
たとえば、12 × 14。例によって、手を開いた、じゃんけんのパーの形から、指折り数える。10 まで行くとまたパーに戻るので、12 だと親指と人差し指の 2 本だけが折れている状態。14 では親指、人差し指、中指、薬指の 4 本が折れている。
折れている指の本数を数える。2 + 4 で 6 だ。これを10 倍して 60 と覚えておく。
次に折れている指の本数同士を掛ける。12 側は 2 本、14 側は 4 本だから、2×4 = 8。
さっきの 60 に今の 8 を足してから、さらに 100 足す。
60 + 8 + 100 = 168 ( = 12 × 14 )
簡単に証明できる。10 から 15 までの数は 10 + a と書ける。ここで、a が折れている指の数だ。10 から 15 までの二つの数を掛けるということは、10 + a と 10 + b を掛けるということだから、
( 10 + a) × ( 10 + b ) = 100 + 10 × (a + b ) + a × b
つまり、折れている両手の指の本数の和、( a + b ) を 10 倍して覚えておいて、折れている指の本数同士の掛け算、a × b をして、さっき覚えた数 10 × ( a + b ) に足して、最後に 100 を足せば、確かに (10 + a ) × (10 + b) になっている。12×14 だったら、a=2、b=4としてみればよい。
大学には、いつもは自家用車で通っているが、久しぶりに JR を使う。当地では JR は電化されていないので、人々は JR のことを「汽車」と呼ぶ。街中は JR と異なり路面電車が走っているので、人々は路面電車のことを「電車」と呼ぶ。きちんと区別している。
どうだ、すごいだろ、この知恵。
都会と違い、頻繁には汽車は来ない。汽車の時刻に合わせて駅に向かう。しかし、都会と違い、ダイヤに拘泥しない。今日は雨だから、きっと汽車は遅れてやって来る。
安全第一、30 秒遅れたとかで人命が失われるような事故は起きない(と思う)。運転手さんをいつも間近に見れるが、いつでもきちんと指差し確認しながら運行している。エライ。地方万歳!!
安全第一、ちょくちょく汽車は遅れる。無人駅でも何故か放送は流れる。かなり前だが、「列車は少々遅れています」という放送があったが、待てど暮らせど汽車は来ない。ようやく来たから乗ったら、乗るつもりの汽車はキャンセルされていて、次の列車が、しかも遅れてやって来たことがある。先週は「列車妨害の為、列車は少々遅れています」という放送があって、かなり遅れた。どんな妨害があったのか、あとで JR 四国のホームページを見たが、「現在、遅れ等の情報はありません」と出ていた。30 分までのダイヤの乱れは、乱れの範疇に入らない。健全な生活環境が未だ保たれている。
無人駅で汽車を待つ。予定通りの時刻に「間もなく、下り列車が参ります。」のアナウンス。駅で待つ人たちがそろそろ来るなとホームで身構える。狭いホーム、その前を、雨を蹴散らし猛スピードで特急が通過していった。そのあとに、「OO線で発生しました停電のため、列車は少々遅れています。」のアナウンス。単線なので、特急が停車する次の駅で上りの列車と行き違い、それが目の前を通り過ぎて終着駅についてから、やおら目的の下り各駅停車がその駅を出発する手筈なので、しばらく駅で時間が出来た。
5 から 10 までの数同士の掛け算は指でできた。10 から 15 までの数同士の掛け算も指でできた。ということは、15 から 20 までの数同士の掛け算も同じようにしてできるのではないかと思い、汽車の待ち時間に駅で考える。予定時刻に汽車が来ないので、駅には通学の高校生たちが増えていた。両手の指を折りながら、ぢっと手をみる、変なおっさんが居るのはさぞかし気味が悪かっただろう。
10 台同士の数の掛け算は第 20 回で記した方法で暗算できるので、その答えに会うような指の組み合わせを考える。第 20 回でやったように、例えば、16 × 18 だったら 16に相方の 18 の 1 の位の数 8 を足してから 10 倍しておく。16 + 8 = 24 だから、240。これに 1 の位同士の数を掛けてから、さっきの 240 に足す。6 × 8 + 240 = 48 + 240 = 288。さぁ、立っている、または折れている指の本数から 288 が出るように、ぢっと手をみる。考える。指折り数えると 16 では 1 本指が立っている。18 では立っている指は 3 本。
① 立っている指の本数を足して 20 倍して覚えておく。1 + 3 = 4 の 20 倍だから80。2 × 4 は知っていることになっている( 5 までの数同士だから)。
② 次に折れている指の数を掛ける。16 だと 4 本折れていて、18 だと 2 本折れているので、4 ×2 = 8 。
③ さっき覚えておいた 80 に足すと、88。
④ 最後に 200 をたす。88 + 200 = 288 (=16 × 18 )。
正しい。他の数でもチェック。正しい。いけるぞ。
汽車に乗る。調子に乗る。20 から 25 までの数同士の掛け算を手の指を使ってできるか挑戦する。例えば、22 × 24。指折り数えると、22 では 2 本の指が折れている。24 では 4 本折れている。
ぢっと手を見る。
① 折れている指の本数を足して 20 倍する。( 2 + 4 ) × 20 = 120。
② 折れている本数同士を掛ける。2 × 4 = 8。
③ さっきの 120 に足すと、128。
④ これに 400 を足す。
528 だ。確かに 22 × 24 = 528。他の数でチェック。正しい。
今度は折れている指の本数しか使わない。10 から 15 までの数同士の掛け算の時と同じだ。なんか規則が見えてきた。が、これ以上暗算できない。汽車は大学の最寄り駅に着いた。ここで、ひとまず終了。
研究室に到着してから、見えてきた規則を早速、整理しておく。
(A) ◇十五から△十(ただし、△ = ◇ + 1 )までの数同士の掛け算では、立っている指の本数を足して、「10 の倍数のいくばくかの数」を掛け、折れている指の本指数同士を掛けて、さっきの数に足し、最後に「100 の倍数のいくばくかの数」を足している。「10 の倍数のいくばくかの数」は、どうやら△十のようだ。△十は(◇ + 1 ) × 10と同じ。「100 の倍数のいくばくかの数」は、△十と(△―1)十を掛けた数の様だ。◇十の言葉では(△=◇ + 1 )だから、((◇ + 1 )十) × (◇十)。さっきの 16 × 18 の時には、◇は 1 だ(△は 2 )。立っている指の本数の和 4 を 2十 ( つまり20 ) 倍した。最後に10×20 (=200 ) を足した。
(B) △十から△十五までの数同士の掛け算では、折れている指の本数を足したものに「10 の倍数のいくばくかの数」を掛け、これまた折れている指の本数同士を掛け、さっきの数に足しておき、最後に「100 の倍数のいくばくかの数」を足す。立っている指の本数は使わない。今度は「10 の倍数のいくばくかの数」は△十。「100 の倍数のいくばくかの数」は ( △十) × ( △十 ) だ。さっきの 22 × 24 では、△は 2 なので、折れている指の数の和 6 に 20 を掛けた。最後に 20 × 20 ( = 400 ) を足した。
最後にもう一度整理。パーから指折り数えて、折れている指の数を a、b とする。立っている指の数はそれぞれ 5-a、5-b、これらを p ( = 5-a )、q ( = 5-b ) としておこう。
◎ 10 n + 5 から 10 n + 10 までの数同士の場合
(10 n は 10 × n のこと。n は 0 から 9 までの整数)
指折り数えると
( 10 n + 5 + p ) × ( 10 n + 5 + q )
を計算することになる。左右の手に立っている指の本数が p と q。掛け算を実行する。
( 10 n + 5 + p ) × ( 10 n + 5 + q )
= ( 10 n + 5 ) × (10 n + 5) + (10 n + 5 ) × (p + q ) + p × q
= ( 100 n × n +100n + 25 ) + ( (10 n +10 ) × (p + q ) + ( 5 -p ) × ( 5-q) )-25
= 10 n × ( 10 n + 10) + 10 × (n+1) × ( p + q ) + (5-p) × (5-q)
こうして、最後の式の真ん中、10 × (n+1) × ( p + q ) は、立っている指の本数の和 ( p + q ) に、◇十五から△十の場合の△(=◇ + 1 )を 10 倍している。これに最後の (5-p) × (5-q) を足しているが、(5-p)、(5-q) は 5 から立っている指の数を引いているので折れている指の数だから、折れている指の本数同士を掛けたことになっている。最後に初項 10 n × ( 10 n + 10) は (◇十)×((◇ + 1 )十)。これを足しておしまい。これで、(A) は示せた。
◎ 10 n から 10 n + 5 までの数同士の場合 (n は 1 から 9 までの整数)
指折り数えると
( 10 n + a ) × ( 10 n + b )
を計算することになる。左右の手で折れている指の本数が a と b 。掛け算を実行する。
( 10 n + a ) × ( 10 n + b )
= 10 n ×10 n + 10 n × ( a + b ) + a × b
今度はやさしい。最後の式の真ん中、10 n × ( a + b ) は、折れている指の本数の和 (a + b ) に、△十から△十五の場合の△( = n) の 10 倍。これに最後の項 a × b を足しているが、これは折れている指の本数同士の掛け算だ。最後に初項 10 n × 10 n は (△十)×(△十)。これを足しておしまい。これで、(B) も示せた。
スマホなんて持ってないので、空き時間に web を見ることもない。汽車が遅れて、ぽっかり時間が出来たら、普段考えないことが考えられる。汽車が遅れても、良いこともあるものだ。
55.走行中はシートベルトをお締め下さい
高速バスに乗る。前の席に付いている網状の物入れみたいなところに、「走行中はシートベルトをお締め下さい」という札が入っており、「時速60 kmで衝突すると、高さ14 m から飛び降りた衝撃と同じです」といった内容のことが書かれていた。第10回で導いたエネルギーの保存法則を使って確かめてみる。
時速60 km ということは、秒速にして
60 km / h = 60 × 1000 m / (3600 秒(s)) = 100 / 6 [m/s] = 16.7 [m/s]
およそ、秒速 16.7 m。
高さ 14 m から飛び降りる。飛び降りる際の位置エネルギーは mgh。m は飛び降りる人の質量、h は高さ14 m、g は重力加速度 9.8 m/s2 。これが地表面ですべて運動エネルギー mv2 / 2 になるとすると
mgh = mv2 / 2
つまり
v = √2gh
だ。ルート2gh。数値を入れると
v = √2×9.8×14 [m/s] = 16.56 [m/s]
およそ、秒速16.6 m。確かに時速 60 kmで衝突する直前の速さとほぼ等しい。
高速バスの中の安全のしおりにも、正しいことが書いてあることを確かめて満足しながら高速バスでの移動は続く。
54.オーストラリアと寺田寅彦
オーストラリアで国際会議(国際学会)があり、自分の研究の口頭発表ができることになったので、出かけることにした。正直、南半球に行くのは初めてなので、そちらの興味の方が強かった。9月半ばのことだ。時差は30分から1時間程度だが、季節が逆という不思議な体験をしてみたかった。
アデレードという町で国際会議は開かれた。シドニーで飛行機を乗り継いでアデレードまで飛んだが、なんか感覚としては、四国は土佐の東洋町から安芸市くらいのつもりだった。ところが、飛行機で2時間ちょっとかかる。オーストラリア、広い。

お昼時に南に向かって街を歩いていると、自分が歩く方向、南側に影が伸びている。自分の影を辿って南に向かうのは、新鮮な感覚だった。太陽は北にあった。太陽は東からのぼり、北側を通って西に沈む。さすが南半球。
南半球に行くことは稀だろうから、奥さんと中学生の子供と出かけた。2人は先に帰るので、3日ほどだけ中学校は休ませることにした。息子は水泳をやっているので、飛行機とあわせて5日も泳がないというのも何なんで、アデレードでプールを見つけて連れて行って、一人で泳がせた。一つのレーンを往復するのだが、日本はレーンの右側を泳いですれ違うのに、オーストラリアは逆だった。息子はそのことを最初は知らずに日本式に泳いでいたが、だんだん混んできて1レーン2人で泳ぐことになった時、オーストラリアのおじさんに、泳ぐ方向が反対だと注意されていたようだった。ガラスがあるので観覧席からは全然聞こえないけれど。しかし、そのおじさん、息子の泳ぎの上手さに驚いたようで、そりゃあ、四国大会では1位か2位を取り、全国大会の標準記録を切って東京辰巳国際水泳場で泳いできたこともあるのだから上手くて速いのは当たり前なのだが、兎に角ビックリしたのだろう、息子になんか話しかけて、さっきまでは、しかめっ面で注意していたのに、笑顔まで出して話し始めていた。息子は中学1年なので英語はそうできるとも思えないが、あとで聞くと、どこから来たのかとか、Japanと答えると東京かとか聞かれたりとか、それなりに受け答えして会話していたらしい。まぁ、それだけでも来た甲斐あって、いい経験になったか。
二人が帰国した後に自分の講演も済ませた。国際会議最終日に講演を聞いていると、原子核物理の医療への応用のところで、粒子線治療のブラッグピークの話が出てきた。加速された粒子を体に当てると、最初、粒子は体表面を透過するのに、あるところで急に吸収される。これをブラッグピークと言う。体の表面から癌などの患部までの深さを知っておくと、照射する粒子のエネルギーを調整してブラッグピークを幹部の深さに合わせ、患部に粒子線が吸収されるようにして治療する。この話の流れで、「ブラッグピークは、ここアデレードで1904年に発見されたのです」と講演者が話し、驚いた。さすがにそこは英語でも聞き取れた。へぇー、そうだったのね。ブラッグピークはブラッグの親の方によって、アデレードで発見されている。
講演の後、アデレード市内をアデレード大学の方へ散歩しているときに、胸像を見つけた。ブラッグ親子の胸像だった。ブラッグ親子はX線回折を利用して結晶構造を解析する方法により、ノーベル賞を得ている。


ブラッグ父 ブラッグ子
ところで、1913年、高知の生んだ物理学者、寺田寅彦は「On the Transmission of X-Rays through Crystals(結晶を通してのX線の透過について)」という論文を東京数学物理学会の学術誌に英文で書いている。その前に、同じ1913年だが、「X-Rays and Crystals(X線と結晶)」という論文も書いていて、Natureという海外の学術誌に掲載されている。ところが、同じ研究がブラッグ親子によって為されていた。彼らは、「結晶による短波長電磁波の回析」という題で1912年11月11日にケンブリッジ哲学協会で口頭発表しており、さらに1913年1月10日付けでProceedings of Cambridge Philosophical Societyという学術雑誌に論文が掲載された。寺田寅彦は、丁寧に、東京数学物理学会の学術誌に掲載された自分の論文の最後に、脚注として「After the paper was read, I have received the paper of Mr. W. L. Bragg entitled “The diffraction of short electromagnetic waves by a crystal”, read before the Cambridge Philosophical Society on Nov. 11, 1912, and printed on Jan. 10, 1913, and became aware that my way of reconstructing Laue's photograms and of explaining the shape of the spots on them was essentially not new.」と記した。自分より先にブラッグ親子が自分と同じことをしていたと公正に記載したのだ。「私の方法は・・・not new (新しくなかった)」。
ブラッグ親子は1915年、第15回のノーベル物理学賞を得る。
寺田先生は漏れた。
53.ホームランが打ちたい
昭和時代を3分割していうならば、昭和後期が始まった頃のこと、スポーツ観戦と言えばテレビのプロ野球くらいしかなかった。地域性によるが、六甲おろしが流れていた。通っていた銭湯の下駄箱は、いつも田淵の背番号 22 だった。
贔屓の球団は、自分が生まれてから一度も優勝していなかった。ところが、大学 2 年のとき、優勝してしまった。21 年振りの優勝であった。中西が最後に投げて優勝を決めた試合は長引き、友達の下宿で翌日のドイツ語の授業の予習会を 4 人で行う曜日だったのだが、さすがに遅れて参加した。祝勝のビールを買い込んで。「どうせ遅れてくると思った」と、広島出身や盛岡出身の友達には大目に見てもらえた。
バース・掛布・岡田の最強打線の頃だった。それを過ぎると、一度優勝してしまったこともあり、急に興味がしぼんだ。それ以降、高校野球を含めても、あまり野球は見ない。
ある日、研究室の外線電話が鳴った。どうせ、「東京で投資のマンション買いませんか」の類だろうと思って、極めて不機嫌なトーンで電話に出ると、子供が水泳の全国大会で東京辰巳の国際水泳競技場で泳いでいたが、そっち方向にある信頼のおける某所からの電話で、トーンを戻して話を聞いてみると、ホームランを打つ企画をしているのだが、ホームランを打てない子でも打つ方法は無いものか、しっかり練習して挑戦するのだが、どうしても打てなかった場合、ブログの 50 回にあった「スーパーボールの衝突」なんかを利用して、ホームランが打てない子でも打たせてあげられないものか、との内容の電話であった。スーパーボールは多段階の衝突を考えると、どんどん速さが早くなる(50 回参照)という話だったのだが、さて、それと同じ原理を野球のバットに仕込めるものか、ちょっとアイデアがなかった。とりあえず、野球の統一球は跳ね返り係数(反発係数)が決まっているので、反発係数の大きな素材で実験してみたら、程度の返答しかできず、その旨お話しして電話を措いた。
言った手前、そのあと、野球のボールをバットで打ったらどうなるかを、反発係数を変えたらどれくらい飛距離が伸びるかを中心に考えてみた。図1 の大きい円がバットの断面、小さい円がボールの断面とする。図で左向きに速さ v [m/s] で飛んできたボールを、バットを右向きに速さ V [m/s] で振って当てる。バットとボールの接触点とバットの中心を結ぶ線が、図のように水平面と角度 θ を持って衝突したとしよう。水平方向をx 方向、鉛直上向き方向を y 方向と呼ぶ。
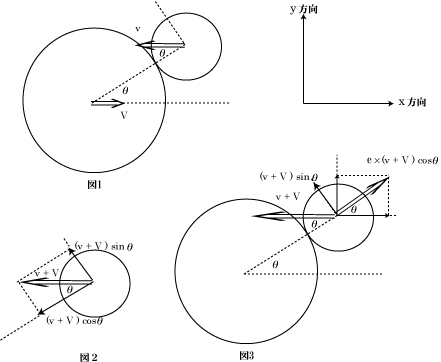
図2 はバットの静止系でボールを見たものだ。バットに乗っかって考えると、ボールはバットに向かって速さ v + V で飛んでくるように見える。バットとの衝突面に垂直方向の速さの成分は、図の様に ( v + V ) cosθ となっている。一方、衝突面に沿った速さの成分は (v + V ) sinθ である:
バットの静止系から見て、
衝突直前の速さの衝突面に垂直な成分 ( v + V ) cosθ
衝突直前の速さの衝突面に平行な成分 ( v + V ) sinθ
衝突面に垂直な方向の速さの成分は、衝突直後には、跳ね返り係数(反発係数)を e と書くと、e の割合で遅くなっている。もちろん 0 ≦ e ≦ 1だ。反発係数の定義は、衝突面に垂直な速度成分に対して
反発係数=(衝突後の2物体の相対速度の大きさ)
÷
(衝突前の2物体の相対速度の大きさ)
と言える。だから、バットの静止系で見て、衝突直後の速さの衝突面に垂直な成分は、
e×( v + V )cosθ となる。衝突面に沿った、衝突面に平行な速度の成分は変わらない。
バットの静止系から見て、
衝突直後の速さの衝突面に垂直な成分 e×( v + V ) cosθ ・・・(1)
衝突直後の速さの衝突面に平行な成分 ( v + V ) sinθ ・・・(2)
図3で、ボールから右斜め上方向に向かう2重矢印⇒が(1)、左斜め上を向いた矢印→が(2)だ。こうして、衝突直後にバットに対して持つボールの速さの水平方向の成分
vx0バット と、鉛直成分 vy0バット は、図3から
vx0バット= e ( v + V )cosθ×cosθ - ( v + V )sinθ×sinθ
vy0バット= e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ
と読み取れる。今度は、バットの静止系から私たちの居る本当の静止系に戻ろう。バットの静止系はバットとともに速さVで水平右向きに動いていたので、本当の静止系に戻すときには水平右向きの速度 V を加えればよい。私たちの静止系から見て、ボールはバットで打たれた直後、
vx0 = e ( v + V )cosθ×cosθ - ( v + V )sinθ×sinθ + V ・・・(3)
vy0 = e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ ・・・(4)
という初速度でバットを離れるということだ。あとは、ニュートン方程式を解いて、飛距離を求めればよい。高等学校の物理の授業では「公式」を使って求める。大学に入って物理を専攻すると、1 回生ですぐに微分方程式としてのニュートン方程式を解いて求める。
(質量)×(加速度)=(力)
なので、ボールの質量を m [kg] 、水平方向の速度を vx [m/s]、鉛直方向の速度をvy [m/s]と書くと、水平の x 方向の運動方程式は
m dvx/dt = 0 ・・・(5)
となる。ここで、dvx/dt は vx を時間 t で微分したもので、速度の時間変化が加速度なので、加速度の x 成分である。水平方向に力は働かないので、右辺は零だ。そうそう、空気抵抗は無視しておこう。
鉛直方向には重力 mg が働く。ここで、g は重力加速度で、9.8 m/s2。下向きに力が働くので、負号に注意して、運動方程式は
m dvy/dt = -mg ・・・(6)
となる。(5)式は簡単で、vx に時間変化が無いと言っているのだから、
vx = (一定)= vx0
だ。すなわち、水平方向には初速 vx0 のまま、飛んでいく。ボールの位置 x の時間変化が水平方向のボールの速度 vx になるので、位置 x は速さ(vx) × 時間(t) なので、
x = vx0 × t ・・・(7)
でわかる。
さて、鉛直方向の(6)式を解くと、
vy = -gt + vy0 ・・・(8)
が得られる。実際に(8)を t で微分すると
dvy/dt = -g
が得られるが、これは(6)で両辺共通の m で割ったものに他ならない。また、(8)で時間 t = 0 の初期時刻では確かに初速 vy0 になっている。鉛直方向のボールの位置 y を求めよう。位置 y の時間変化が速度 vy であるので、
dy / dt = vy
だから、右辺に(8)を代入して
dy / dt = -gt + vy0 ・・・(9)
これをyについて解くと(積分すると)
y = -g×t2 / 2 + vy0×t ・・・(10)
が得られる。実際に t で微分したら(9)になることを確かめればよい。また、t = 0の、バットとボールが衝突した時間では、鉛直方向の高さを零とした。ボールの打点の位置を基準の高さ 0 と決めたということ。
解いた答え(7)と(10)から、ボールの飛距離がわかる。飛距離の位置を打点の高さ y = 0 としておこう。(10)から y = 0 になる時間は、左辺の y に 0 を入れて
0 = (-gt / 2 + vy0 ) t
とできるので、
t = 0 または t = 2×vy0 / g
である。t = 0 は明らかに打った瞬間で、打点の高さは確かに 0 だが、飛距離を求めたいので、ボールが上がって落ちてくるまでの時間、t = 2×vy0 / g を取る。この時間でボールは高く上がって落ちてくるが、その際、水平方向にはどれくらい飛んだかというと、(7)式だから
x = vx0 × t = 2 vx0 vy0 / g
= 2×[e ( v + V )cosθ×cosθ - ( v + V )sinθ×sinθ + V]
×[e ( v + V )cosθ×sinθ + ( v + V )sinθ×cosθ]/ g
三角関数の公式を使ってちょっと整理しておくと
x = [( v+V ) / g ] ×(1+e)×sin 2θ×[( v + V )×( e (cosθ)2 -( sinθ)2 ) + V] ・・(11)
が得られる。
さぁ、数値を仮定して飛距離を見てみよう。もう一度確認だが、空気抵抗は無視している。プロ野球のボール、統一球というやつは、反発係数が 0.4034 から 0.4234 の間だそうだ。間を取って
e = 0.41
としておこう。ボールの速さは、時速 150 km とかだと、よう打たんので、時速 120 km としてみる。それでも打ち返せないだろうなぁ。でもまぁ計算のため。
vx0 = 120 km / 時 ≒ 33.3 m/s
バットの長さは 106 cm 程度だそうだ。バットを持って体を回転させてバットのヘッドに速さVを持たせる。体の中心軸からバットを持つ手まで 40 cm 、バットの先から20 cm のところにボールが当たったとして、体の中心軸からおよそ r = 1.2 m のところにボールが当たったとする。バットを半回転、180 度回転するのに 0.2 秒でフルスイングしたとしよう。このとき、与えた角速度は ω= π/0.2 rad/s。π は円周率で、角度をラジアンで測っている。そうしたら、バットの速さは
V = r×ω = 1.2×π/0.2 ≒ 18.8 m / s ≒ 67.8 km / 時
時速 68 kmだ。重力加速度は g = 9.8 m/s2 を使うので、(11)式から飛距離 x [m] が、ボールがバットに当たった角度θの関数として求まる。数値計算の結果を描いてみよう。
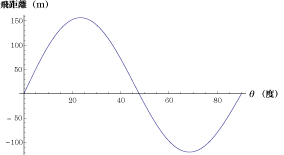
横軸が普通の単位、「度」で測った角度、縦軸が飛距離だ。角度 14 度で飛距離は 127 mとなり、角度 23.4 度のとき飛距離が最大で157 m になる。角度 33 度で再び飛距離は126 m 程度になる。フェンスの高さも考えないといけないが、14 度から 33 度でバットをボールに当てると、ホームランになりそうだ。角度 47 度を超えたあたりから飛距離がマイナスになるが、まぁ、キャッチャーのファウルフライというところだろうか。
お題は、「ホームランが打ちたい」だった。普通にやっていては打てない(かもしれない)から、なんとか打とうという企画であった。とりあえず、反発係数の大きな場合を考えてみよう。スーパーボールを落下させて、床面に衝突したあと、最初の高さの 80 % 位まで戻ってきたという実験があるそうだ。高さ h [m] から落とすと、エネルギー保存則を使うと、床面に衝突する直前の速さは √(2gh) となることがわかり、この後 0.8 h の高さまで上昇するので、衝突直後の速さは √(2g×0.8h) となるので、反発係数は
√(2g×0.8h) / √(2gh) ≒ 0.89
で、およそ 0.9 だ。スーパーボールでホームランを狙おう。
反発係数を 0.9 にして計算し直して見る。
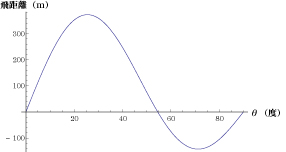
今度は、角度 6 度で飛距離は 136 m、角度 25.8 度で最大の飛距離 373 m がでる。角度47 度で 129 m まで落ちるが、120 m を超えているので、十分ホームランだ。当たる角度が少々悪くてもホームランが狙える。
時速 120 km のボールを打つのは難しいし、フルスイングしてもバットの速度が速くならないかもしれない。空気抵抗もあるだろう。
だけど、今までの条件で飛距離が最大 373 m 出るんだから、条件を緩めても、きっとホームランは打てる、よ。
と、願っておこう。
52.集合
小学生の時、算数の授業に「集合」が取り入れられた。取り入れられて間もない頃だったと思う。「AまたはB」とか「AかつB」とかあって、ベン図なんてものを習った。小学生にも小学校の先生にも、なんで小学生に集合論と思ったことだろう。
今から考えるに、思いっきり、ニコラ・ブルバキの影響だったんだと思われる。
ニコラ・ブルバキ。フランスの幾人かからなる数学者集団で、数学を基礎から再構成しようとしていたようだ。最も基礎に置いたのが「集合論」だったと思う。大学生になって生協の本屋にブルバキの本がずらりと並んでいた。どうせ読まないだろうが、あまりに壮観なので一寸欲しかったが、物理を専門にするつもりだったので、そこまで手が回らなかった。
「数」をどうやって基礎づけるか。数学者というのは、当たり前のように思えることまで考える人たちだ。大学時代、学科が分かれていなかったので語学の授業で「クラス」のようなものが出来上がっていたのだが、そのおかげで物理だけではなく、化学志望や数学志望の友人などができた。数学志望の友人から、「1」「2」「・・・」と、数の概念を把握するのは実は難しいことなんだと聞かされていた。リンゴが1個、ミカンが1個、人が一人、具体的に違うのに、「1」という共通項があることを理解するのは難しいことだと言っていた。当時は何のことかよくわからなかったが、リンゴが1個、ミカンが1個、人が一人、全部抽象化したときの「1」を、どうやって、リンゴとかの個別、実態に頼らずに「1」を導入するか、ということを、数学の解っていない物理志望のやつに言いたかったのかもしれない。
そこで、どうやら、集合論が必要になるようだ。数学者じゃないし、勉強してないから間違っているかもしれないが。
「りんごが1個ある集合」とか、「人がひとり居る集合」とか考えて、その要素の数が「1」と言ってもダメならしい。要素に個性がある。抽象化されていない。
そこで、「要素が何もない集合」というのを考える。「空集合」だ。記号では∅。具体的に何も入ってないんだから、リンゴでもミカンでも人でもない。具体的でないんだから抽象的だ。「何もない」。そこで、空集合に「0」を対応させる。
次は、1。要素が一つの集合を考えたいが、リンゴとかの具体はダメ。そこで、「空集合を要素に持つ集合」を考える。考えている集合の要素はただ“一つ”。その要素がまた集合で、それが「空集合」。集合の集合を考えるわけだ。集合の要素を中括弧 { }の中に書くと、{∅}という集合だ。「空集合を要素に持つ(集合の)集合」を考え、これに「1」を対応させる。
2 はどう定義するか。具体的でない要素を“2つ”持たせる。空集合φと、空集合を要素に持つ集合{∅}を考え、これらの集合を要素に持つ(集合の)集合を考える。要素を書けば{∅, {∅} }ということだ。具体でない抽象的な要素を持つこの集合に「2」を対応させる。
あとは、同じ。「3」は今まで導入した集合を要素に持つ集合{∅, {∅}, { ∅, {∅} } }を考えて、「3」を定義する。
以下、順々にして、0を含む自然数は定義できる。
数学者というのはややこしいことを考えるものだ。おかげで、小学生から集合を学ぶことになった。
51.原子核のアルファ・クラスター
水素からはじまって、ヘリウム、リチウムと、原子核に含まれる陽子の個数が増えていくにつれ、特有の元素として元素記号が与えられている。普通の水素原子核は陽子が1つからできていて、元素記号は H。ヘリウム原子核は陽子 2 つと中性子 2 つからできているものが多く、元素記号は He。陽子 2 つ、中性子 1 つからなるヘリウム原子核もあり、これはヘリウム 3(3He)と呼んでいる。普通の奴は、ヘリウム 4(4He)。原子核に含まれる陽子の個数を原子番号と呼び、原子核に含まれる陽子と中性子の個数を足した数を質量数と呼ぶ。質量数を元素記号の左上に記す。元素の種類は原子番号で決まる。
原子核ではヘリウム 4 は極めて安定で、ヘリウム 4 を纏まりとして、原子核を考えることもできる。例えば、安定な炭素 12 の原子核は陽子 6 個と中性子 6 個からなるが、ヘリウム 4 が 3 個からなると考えても良い状態がある。また、安定な酸素 16 の原子核は陽子 8 個と中性子 8 個からできているが、ヘリウム 4 が 4 個からできているとした方が理解できる状態もある。
ヘリウム 4 の原子核は安定なのだが、陽子の個数が一つ増えたリチウム 5(5Li)とか、中性子の数が一つ多いヘリウム 5(5He)は、原子核としては極めて不安定である。そうすると、宇宙ができた直後とか、恒星の内部で、軽い原子核から順々に重い原子核を作ろうとしても、“5”のところで行き詰まる。リチウム 5 とかヘリウム 5 とかができてもすぐに壊れてヘリウ ム 4 と陽子、または中性子に戻ってしまい、ヘリウム 4 より重い原子核ができないことになってしまう。
そこで、ヘリウム4原子核は安定なのだから、これが 2 つぶつかって融合してベリリウム 8(8Be)という原子核になれば良いと考えたくなる。ところが、陽子と中性子をあわせて 8 個持つ原子核もおしなべて不安定である。ベリリウム 8 も、できてもすぐに壊れる。寿命が極めて短い。大学 3 回生のときにグループに分かれて半年かけて行う課題実験で、タンデム・バンデグラフ加速器なるものを使ってベリリウム 8 の寿命と偶奇性を測定する実験というのを行った。結果は、ベリリウム 8 が存在しても寿命は10-22秒程度という結論だった。この世で最も早い光が原子核一つの端から端まで進む時間がおよそ10-23秒程度。相互作用がベリリウム 8 の端から端まで伝わる程度で原子核が壊れてしまうのだから、到底存在するとは言えない。
では、原子核はヘリウム 4 までしかできないのか。私たちは水やらタンパク質でできているが、それらの構成要素としては、原子番号 6 の炭素(C)や、原子番号 8 の酸素(O)が多量に存在している。私たちが存在するのだから、原子核の陽子・中性子の個数の和である“質量数”が5以上の原子核が出来てくれなくては困る。
そこで、フレッド・ホイルという人が、ヘリウム 4 が二つ衝突して極めて短時間だがベリリウム 8 の状態になり、それが壊れて 2 つのヘリウム 4 になる前にもう一つヘリウム 4 が衝突して炭素 12(12C)ができると考え、炭素 12 の原子核にはヘリウム 4 が 3つに対応したえエネルギーのところに共鳴状態があると提唱した。これは「ホイル状態」と名付けられたが、実験的に実際に見つかる。こうして、恒星の中でヘリウム 4 から炭素 12 が作られる道が見つかり、あとはヘリウム 4 を順次くっつけて、酸素16(16O)、ネオン 20(20Ne)、マグネシウム 24(24Mg)、けい素 28(28Si)などなど、重い原子核、つまりは重い元素が合成されていくことが理解された。
ちなみに、フレッド・ホイルは、ガモフが大爆発で宇宙が出来たと提唱した時、ちょっと蔑ずんで、その大爆発のことを「ビッグ・バン」と呼んだ人だ。
大学院生のとき、炭素 12 は安定なのに、ベリリウム 8 は何で安定でないんだろうと思っていた。あまり正しくはないかもしれないが、炭素 12 もヘリウム 4 が 3 つから出来ていると仮に考えると、簡単な理屈がある。
ヘリウム 4 の原子核、いちいち面倒くさくなってきたので、歴史的な経緯からヘリウム 4 の原子核のことを「アルファ粒子」と呼ぶことにするが、2 つのアルファ粒子に引力が働くと考える。この引力による 2 つのアルファ粒子間の位置エネルギーを-Vとする。マイナス記号を付けたのは引力でエネルギーが得をするから。アルファ粒子の運動エネルギーを T と書くと、アルファ粒子は 2 つあるので、ベリリウム 8 の運動エネルギーは T + T = 2T と、2 倍の T だ。しかし、ベリリウム原子核のことだけを考えるのならば、ベリリウム原子核は静止していると考えた方がよい。これは、ベリリウム原子核の重心運動を分離して、重心運動の運動エネルギーを別に考えるということだ。正確にいうと、2 つのアルファ粒子からなる系を重心運動と相対運動に分けるということ。その上で、重心は静止しているとしたらよい。重心と言ってきたが、正確を期すと、「慣性中心」。ベリリウム 8 原子核の運動エネルギー 2T のうち、T が重心の運動エネルギーになる。こうして、重心運動を除いて、「静止」したベリリウム 8 原子核の全エネルギー(= 運動エネルギー + 位置エネルギー ) は
T + (-V ) = T - V
となる。しかし、ベリリウム 8 の原子核は安定に存在しないので、このエネルギーは正または 0 のはずだ。安定だったら引力で束縛されていて、全体のエネルギーが負になっているはずだから。まぁ、きわめて短時間はベリリウム 8 が存在すると考えて、カツカツ 0 と考えておこう:
T - V ≒ 0 ・・・(1)
では、炭素 12 ではどうだろうか。アルファ粒子が 3 つからなると考えると、3 つのアルファ粒子の運動エネルギーは、T + T + T = 3 T 。ただし、このうち、重心運動の運動エネルギー T を除くと、3 つのアルファ粒子の相対的な運動のエネルギーは、3 T - T = 2 Tとなる。では、アルファ粒子間の位置エネルギーはどうなっているか。3 つのアルファ粒子に、1、2、3と名前を付けると、1-2 間の相互作用の位置エネルギー(-V)と、2-3 間の相互作用の位置エネルギー(-V)と、3-1 間の相互作用の位置エネルギー(-V)と 3 つ出てくるので、(-V)+(-V)+(-V)= -3 V となる。こうして、炭素 12 原子核の全エネルギーは
2 T + (-3 V )= 2 ×( T - V )- V
≒ - V
となる。ここで、ベリリウム 8 で成り立つ事実(1)式を用いた。こうして、炭素 12原子核の全エネルギーは -V < 0 と負になるので、2 つのアルファ粒子からなるベリリウム 8 原子核は不安定で存在しなくても、3 つのアルファ粒子からなる(と仮定した)炭素 12 原子核は束縛状態として存在することがわかる。
2016 年に、陽子が 113 個ある原子核に名前が付いた。ニホニウム(Nh)と、日本に関係する名称がついた。2004年当時、埼玉和光の理化学研究所にいた森田浩介さん率いるグループが、2004年7月23日に、亜鉛 30 とビスマス 83 の原子核をぶつけて初めて113 番元素を作った。2004年秋、9月27日から30日まで行われた日本物理学会秋季大会の申し込みには間に合わなかったので、急遽追加公演として突っ込んだ。その時、高知大学で行われた物理学会の実行委員をしていたので、学会の何日目か、確か 3 日目だったと思うが、当時、大学で一番収容人数の多い教室であった 210 番教室で行われていたセッションの最後に、追加で森田さんに 113 番元素の発見の講演をして頂いたことを覚えている。113 番元素発見の第一報は高知発であった。その、ニホニウムは 0.002秒でアルファ粒子(α)を 3 個出して壊れる。
278Nh → 266Bh + 3α
または、6 個のアルファ粒子を出して壊れる。
278Nh → 254Md + 6α
どちらにしても 1000 分の 2 秒の寿命、2×10-3 秒の寿命というのは、ベリリウム 8 に比べてはるかに長い。
日本初の元素の誕生に、ほんの微かに、学会発表の教室のアレンジというだけではあるが関われて、high intelligence の誉れである。
50.スーパーボールの衝突
スーパーボールなる、子供が喜ぶ小さいボールが売られている。なにがスーパーかというと、良く跳ねること。アスファルトなんかに叩きつけると、勢いよく跳ね返る。昔、子供の時分には値段はそこそこ高かったので一つ二つくらいしか持っていなかったが、今では100円ショップで大きさも色も、とりどりのスーパーボールがいくつも入って100円+消費税で売られている。
授業で、物体の衝突の問題を扱う際に、面白い実例を見せようと思って、スーパーボールと厚紙で図のようなものを作ったことがある。

大きい方のスーパーボールに、紙で作った円筒をどうにかして貼っておく。その円筒の中に、できれば円筒にぴったりの別のスーパーボールを入れておく。円筒を持って、自由落下させる。そうすると、全体が床に当たって跳ね返った時に、円筒の中に入れたスーパーボールが勢いよく飛び出してくる。
実演してから、計算を、と思ったが、実際に落としてみると、かなりの勢いでスーパーボールが飛び出してくることがわかった。しかも、正確にまっすぐに落とさないと、円筒がまっすぐに上を向かず、少し横に向いたら、向いた方向に目がけて中のスーパーボールが結構な速さで飛び出してくるので、飛び出した方向に人が居たら、かなり危ない。安全性が確保できないので、授業で演示するのは断念。
学生さんにしてもらおうとした計算だけ記しておこう。
物体が衝突したら、普通、エネルギーは失われる。熱になったり、音が生じたり。しかし、スーパーボールは良く跳ねるので、エネルギーは失われずに跳ね返ると仮定しよう。言葉で言えば、「完全弾性衝突」だ。2つのスーパーボールの衝突の前後で、運動量と力学的エネルギーは変化しない。これを頼りに考えてみる。

図の左端のように2つのスーパーボールは地面に向かって同じ速さで落下してくる。下の大きくて重い方のスーパーボールの質量を m1 [kg]、円筒の中に入っている、上の小さくて軽い方のスーパーボールの質量を m2 [kg] としておこう。下のボールが地面にぶつかって跳ね上がる。エネルギーを失わずに跳ね返って跳ね上がるとしたので、地面に当たる直前の下側のボールの下向きの速さを v [m / s] としておくと、地面に衝突直後は下のボールは上向きに速さ v [m / s] となっている。そこへ、上側の軽いスーパーボールがやってくる。図の真ん中の状況だ。お互い、速さ v [m / s] で正面衝突する。上向きを正の方向とすると、下向きの速さは -v [m/s]とマイナス符号(負号)を付けておけばよい。このとき、2つのスーパーボールの衝突後(右端の図)の運動量は、衝突前(図の真ん中)の運動量と同じである。運動量は、(質量)×(速度)なので、
m1 v - m2 v = m1 v1 + m2 v2 ・・・(1)
が満たされる。衝突の前(左辺)と後(右辺)で運動量の総量は変化していないという式だ。また、衝突の前後で物体の位置エネルギーは変化しないので、運動エネルギーだけ考えて、衝突の前後で運動エネルギーが変化しないとすると
m1 v2 / 2 + m2 v2 / 2 = m1 v12 / 2 + m2 v22 / 2 ・・・(2)
となる。それぞれの運動エネルギーは、 ( 1 / 2 )×(質量)×(速度の2乗)。(1)式と(2)式を連立方程式として解いて v1 と v2 をもとの速さ v で表すと、
v1 = ( m1 - 3 m2 ) / (m1 + m2 )× v
v2 = ( 3 m1 - m2 ) / (m1 + m2 )× v ・・・(3)
と得られる。
さて、下側のスーパーボールは上側のスーパーボールより重いとした。そこで、m1 は十分 m2 より大きいとして、得られた(3)式で、m1 に比べて m2 を無視してしまおう。そうすると
v1 ≒ v
v2 ≒ 3 v ・・・(3)
となることがわかる。速さ v2 は上側のスーパーボールの速さなので、地面に衝突する前の 3 倍の速さを持って跳ね上がることがわかる。
実際にやってみると、本当に勢いよく飛びあがるので、面白いが、危ない。
今はきちんと計算してから、下のボールが上のボールより圧倒的に重いと近似した。ちょっとサボって、下のボールは上のボールより圧倒的に重いので、図の真ん中の状況で、下のボールは上のボールが衝突してきても何ら影響されないとしてみよう。下のボールから見ると、上のボールは相対的に速さ 2v で近づいてくる。衝突後は、速さ 2v で下のボールから遠ざかるだろう。下のボールは衝突後も影響されないとしたので、上向きに速さ v で動いている。このボールに対して上のボールは速さ 2v で上向きに動いているのだから、静止している私達から見ると、上のスーパーボールは上向きに速さ 3v で動いているはずだ。きちんと計算してから近似して得られた(3)の結果と同じだ。
今度は、さらに軽いスーパーボールを載せて 3 段重ねにする。2 段目のスーパーボールの速さ 3 v と 3段目のスーパーボールの速さ -v の速度を持った 2 球の衝突になるが、2 段目のスーパーボールの重さより 3 段目のスーパーボールの重さが圧倒的に軽いとすると、今度は 2 段目のスーパーボールから見て 3 段目のスーパーボールは相対的に速さ 3v - (-v) = 4v で衝突してくる。2 段目のボールは重くて 3 段目のボールが衝突してきても何ら影響されず、相変わらず上向きに 3v の速さで動いているとしよう。3 段目のボールは衝突後、2 段目のボールに対して速さ 4v を維持して上向きに離れていくだろうから、2 段目のボールの上向きの速さ 3v に対して、4v の速さで 3 段目のスーパーボールは上向きに跳んでいく。つまり、静止している私達から見て、3 段目のスーパーボールは近似的に速さ 7v (=4v + 3v )で飛び上がっていくはずということだ。
計算上、スーパーボールをどんどん積み重ねておいてから落とすと、一番上のスーパーボールの速さは相当なものになるはずだ。恐ろしい、危険だ。